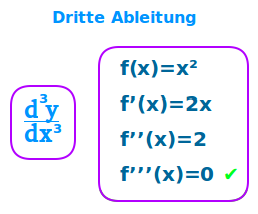
Dritte Ableitung
f'''(x)
Definition
f(x) abgeleitet gibt die erste Ableitung f'(x). Diese noch einmal abgeleitet gibt die zweite Ableitung f''(x) und das noch einmal abgeleitet gibt die dritte Ableitung f'''(x). Hier ist kurz erklärt, wie man die dritte Ableitung bildet und was sie anschaulich bedeutet.
Eine wichtiger Unterschied: Wert oder Funktion?
Das Wort Ableitung wird in zwei ähnlichen aber leicht unterschiedlichen Bedeutungen verwendet. Für f(x)=x² ist f'(x)=2x die sogenannte Ableitungsfunktion. Und f'(4)=8 ist der sogenannte Ableitungswert, auch Steigung genannt, an der Stelle x=4. Beides, die Ableitungsfunktion wie auch den Ableitungswert an einer Stelle nennt man kurz oft Ableitung. In diesem Artikel steht Ableitung für die Ableitungsfunktion f'(x) sowie die höheren Ableitungen f''(x) und f'''(x). Siehe auch Ableitungsfunktion ↗
Wie berechnet man die dritte Ableitung?
Die dritte Ableitung erhält man, indem man f(x) ableitet und das Ergebnis dann wieder ableitet und dieses Ergebnis dann noch einmal ableitet: f(x) = 4x² ⭢ ableiten ⭢ f'(x) = 8x¹ ⭢ ableiten ⭢ f''(x) = 8x° ⭢ ableiten ⭢ f'''(x) = 0 ⭢ siehe auch unter dritte Ableitung bilden ↗
Schreibweisen für die dritte Ableitung
- f'''(x) ist die sogenannte Lagrange-Notation ↗
- d³y/dx³ heißt Leibniz-Notation ↗
Sprechweisen für die Lagrange-Notation
- f'(x) spricht man: f-Strich-von-x
- f''(x) spricht man: f-zwei-Strich-von-x
- f'''(x) spricht man: f-drei_Strich-von-x
Zahlenbeispiel zur Rechnung
- f(x) = x³ ist die ursprüngliche Funktionsgleichung ↗
- f'(x) = 3x² ist dann die erste Ableitung ↗
- f''(x) = 6x¹ ist dann die zweite Ableitung ↗
- f'''(x) = 6x° oder kurz 6 ist die dritte Ableitung.
- Siehe allgemein auch mehrfach ableiten ↗
Kann f'''(x) als Funktion 0 werden?
- Ja, wenn der Grad von f(x) weniger ist als drei.
- Dann wird die gesamte Ableitungsfunktion zu Null.
- f(x) = 2x² ⭢ f'(x) = 4x¹ ⭢ f''(x) = 4 ⭢ f'''(x) = 0
- f(x) = 2x¹ ⭢ f'(x) = 2 ⭢ f''(x) = 0 ⭢ f'''(x) = 0
- Man sagt auch: die Ableitung verschwindet.
- Mehr unter dritte Ableitung gleich null ↗
Die dritte Ableitung und Wendepunkte
- Wenn die zweite Ableitung 0 ist, kann ein Wendepunkt vorliegen.
- Es muss dort aber kein Wendepunkt vorliegen.
- Die dritte Ableitung schafft mehr Klarheit.
- Vorausgsesetzt, die 2. Ableitung war 0, dann gilt:
- 3. Ableitung < 0 ⭢ Wendepunkt liegt vor, und zwar ein LR-Wendepunkt ↗
- 3. Ableitung > 0 ⭢ Wendepunkt liegt vor, und zwar ein RL-Wendepunkt ↗
- 3. Ableitung = 0 ⭢ es ist weiter unklar.
- Tipp: < meint "ist kleiner als"; > meint "ist größer als"
- Siehe auch dritte Ableitung und Wendepunkt ↗