Zweite Ableitung
f''(x)
Basiswissen
f(x)=2x³ einmal abgeleitet gibt f'(x)=6x². Das noch einmal abgeleitet gibt f''(x)=12x. Das ist die zweite Ableitung f''(x) der ursprünglichen Funktion. Die zweite Ableitung hilft zu entscheiden, wo der Graph von f(x) links- und wo er rechtsgekrümmt ist. Zudem hilft sie zu entscheiden, welche Art von Extrempunkt (Hoch- oder Tiefpunkt?) vorliegt. Beide Themen sind hier näher erklärt.
Eine wichtiger Unterschied vorab: Wert oder Funktion?
Das Wort Ableitung wird in zwei ähnlichen aber leicht unterschiedlichen Bedeutungen verwendet. Für f(x)=x² ist f'(x)=2x die sogenannte Ableitungsfunktion. Und f'(4)=8 ist der sogenannte Ableitungswert, auch Steigung genannt, an der Stelle x=4. Beides, die Ableitungsfunktion wie auch den Ableitungswert an einer Stelle nennt man kurz oft Ableitung. In diesem Artikel steht Ableitung für die Ableitungsfunktionen f'(x) und f''(x). Siehe mehr dazu unter Ableitungsfunktion ↗
Definition
- Man hat eine Funktion f(x) gegeben, zum Beispiel: f(x) = 10x³
- Man kann diese Funktion ableiten zu f'(x) =20x²
- Man kann f'(x) selbst ableiten zu f''(x) = 40x
- Das ist die zweite Ableitung.
- Siehe auch ableiten ↗
Sprech- und Schreibweisen
- Variante I: erste Ableitung = f'(x), sprich: f-Strich-von-x
- Variante I: zweite Ableitung = f''(x), sprich: f-zwei-Strich-von-x
- Variante II: erste Ableitung = y', sprich: y-Strich
- Variante II: zweite Ableitung = y'', sprich: y-zwei-Strich
Die zweite Ableitung im Vergleich mit der ersten Ableitung
- Die erste Ableitung f'(x) sagt etwas über die Steigung der ursprünglichen Funktion f(x).
- Die zweite Ableitung f''(x) sagt etwas über die Krümmung der ursprünglichen Funktion f(x).
- Dort wo die zweite Ableitung negative Werte hat ist die ursprüngliche Funktion rechtsgekrümmt ↗
- Wo die zweite Ableitung positive Werte hat ist sie linksgekrümmt ↗
- Wo die zweite Ableitung den Wert 0 hat, kann die ursprüngliche Funktion einen Wende- oder Sattelpunkt haben oder linear (gerade) verlaufen.
[1]">
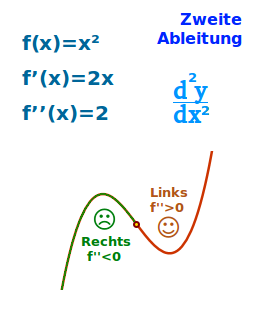
Die zweite Ableitung und die Richtung der Krümmung[1]
- Wo der Graph von f(x) eher talförmige Formen hat (wie ein u) ist er linksgekrümmt, auch konvex genannt.
- Wo der Graph von f(x) eher bergförmig ist, ist er rechtsgekrümmt, auch konkav genannt.
- Setzt man einen x-Wert in f''(x) ein, erhält man Informationen zur Krümmung an dieser Stelle:
- f''(x) < 0 Rechtskrümmung [konkav] ↗
- f''(x) > 0 Linkskrümmung [konvex] ↗
- f''(x) = 0 keine eindeutige Krümmung ↗
Die zweite Ableitung und die Stärke der Krümmung
- Die zweite Ableitung sagt nichts über die Stärke der Krümmung.
- Die Stärke der Krümmung beschreibt das Krümmungsmaß ↗
Die zweite Ableitung und Extrempunkte
- Setzt man den x-Wert von einem Extrempunkt in die zweite Ableitung ein, erhält man weitere Informationen zu dem Extrempunkt.
- Da ein Tiefpunkt immer im Bereich eine Linkskrümmung liegt gilt: zweite Ableitung größer 0 Tiefpunkt ↗
- Da ein Hochpunkt immer im Bereich eine Rechtskrümmung liegt gilt: zweite Ableitung kleiner 0 Hochpunkt ↗
Die zweite Ableitung und Wende- sowie Sattelpunkte
- Ein Sattelpunkt ist ein besonderer Wendepunkt.
- Beiden Punkten ist gemeinsam: hier wechselt die Krümmung von links nach rechts oder umgekehrt.
- An dem Punkt selbst ist der Graph weder links- noch rechtsgekrümmt.
- Der Wert der zweite Ableitung muss dort Null sein. Siehe auch Wendepunkt ↗
Berechnung der zweiten Ableitung
- Die erste Ableitung f'(x) abgeleitet gibt die zweite Ableitung.
- f'(x) = 2x-1 abgeleitet gibt z. B. f''(x) = 2
- f''(x) nennt man auch die zweite Ableitungsfunktion ↗
- Setzt man dort einen x-Wert ein, erhält man den Wert der zweiten Ableitung.
- Mehr zur Berechnung unter zweite Ableitung bilden ↗
Rechenbeispiel zur zweiten Ableitung
- f(x) = 2x³
- f'(x) = 6x²
- f''(x) = 12x
- An der Stelle x=0 erhält man f''(0) = 0. Dort liegt möglicherweise ein Wendepunkt ↗
- An der Stelle x=2 erhält man f''(2) = 24. Dort ist der Graph also linksgekrümmt ↗
- An der Stelle x=-2 erhält man f''(-2) = -24. Dort ist der Graph als rechtsgekrümmt ↗
- Setzt man weitere x-Werte ein, erhält man weitere Informationen über die Krümmung ↗
f(x)=x⁴ als problematischer Sonderfall
- Der Graph von f(x)=x⁴ ähnelt einer Parabel und heißt quartische Parabel ↗
- Der Graph ist von der sichtbaren Form her durchgängig linksgekrümmt.
- Der Graph hat weder erkennbare Wendepunkte noch Geraden.
- Theoretisch müsse der Wert der zweiten Ableitung für alle x-Werte positiv sein.
- Das ist er aber nicht, denn: f''(x) = 12x² und f''(0)=0.
- Siehe auch zweite Ableitung gleich null ↗
Zusammenfassung
- Zweite Ableitung ist kleiner Null ⭢ f(x) ist rechtsgekrümmt
- Zweite Ableitung ist größer Null ⭢ f(x) ist linkgekrümmt
- Zweite Ableitung ist genau Null ⭢ möglicher Wende/Sattelpunkt (weder links- noch rechtsgekrümmt)
- Erste Ableitung war Null, zweite ist negativ: Hochpunkt
- Erste Ableitung war Null, zweite ist positiv: Tiefpunkt
- Erste Ableitung war Null, zweite ist auch null: möglicher Sattelpunkt
- Erste Ableitung war Null, zweite auch, dritte nicht Sattelpunkt ↗
- Erste Ableitung war Null, zweite auch, dritte auch Geradengleichung ↗
- Erste Ableigung ungleich Null, zweite Null, dritte nicht Wendepunkt ↗
Fußnoten
- [1] Lothar Papula: Mathematik für Ingenieure und Naturwissenschaftler. Ein Lehr- und Arbeitsbuch für das Grundstudium. Band 1. 14. Auflage, 2019. ISBN: 978-3-658-05619-3. Verlag Springer Vieweg. Hier das Kapitel: Geometrische Deutung der 2. Ableitung. Seite 372 ff. Siehe auch Der Papula ↗