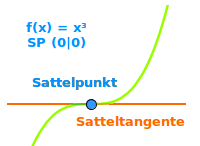
Sattelpunkt
Wendepunkt mit waagrechter Tangente
Basiswissen
Jeder Sattelunkt, sehr treffend auch Horizontalwendepunkt genannt, ist immer auch ein Wendepunkt: an dem Punkt wendet (ändert) sich die Krümmungsrichtung eines Graphen. Gleichzeitig ist die Steigung in dem Punkt immer gleich 0, die Wendetangente verläuft also waagrecht. Das ist hier näher erklärt.
Definition
- Sattelpunkte SP sind Wendepunkte. Sie haben immer eine waagrechte Tangente ↗
- Sattelpunkte gehören nicht zu den Extrempunkte[n] ↗
- Ein übliche Abkürzung ist SP ↗
Eigenschaften
- Die Steigung ist immer Null (per Definition).
- Die Richtung der Steigung bleibt aber vor und nach den SP gleich.
- Was sich an einem Sattelpunkt ändert ist die Richtung der Krümmung ↗
- Die Krümmung ändert sich von links nach rechts oder umgekehrt.
- Jeder Sattelpunkt ist damit immer automatisch auch ein Wendepunkt ↗
- Aber nicht jeder Wendepunkt ist auch ein Sattelpunkt.
Formal
- f'(x) = 0
- f''(x) = 0
- f'''(x) <> 0
Tangente
- Die Tangente an einem Sattelpunkt hat immer die Steigung 0.
- Der Graph dieser Tangente t(x) ist eine waagrechte Gerade.
- Die Tangente schneidet den Graphen f(x) im Sattelpunkt.
- Mehr unter Satteltangente ↗
Berechnung
- Notwendig: Erste Ableitung muss Null sein.
- Notwendig: Zweite Ableitung muss Null sein.
- Notwendig: Dritte Ableitung muss ungleich Null sein.
- Hinreichend: alle drei Bedingungen zusammen
- Mehr unter Sattelpunkte bestimmen ↗
Etymologie
- Der Name ist in Anlehnung an einen Pferdesattel gegeben.