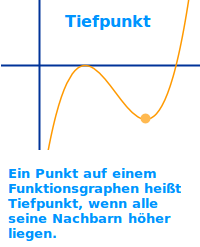
Tiefpunkt
Analysis
Basiswissen
Definition: ein Tiefpunkt im Sinne der Anaysis ist ein Punkt auf einem Funktionsgraphen. In der Umgebung links und rechts von diesem Punkt sind alle anderen Punkte höher. Erklärt werden verschiedene Arten von Tiefpunkten und wie man sie bestimmt.
Was meint "Tiefpunkt" anschaulich?
- Der Graph einer Funktion schlängelt sich oft über das Koordinatensystem.
- Dabei zeigt er manchmal Auswölbungen nach oben und nach unten.
- Die tiefsten Punkte auf einer Auswölbung nach unten heißen Tiefpunkte.
- Direkt links und rechts von einem Tiefpunkt sind nur höhere Punkte.
- Bei Parabeln ist ein Tiefpunkt immer auch ein Scheitelpunkt ↗
Ist diese Definition allgemeingültig?
- Nein, es gibt zwei - leicht - voneinander abweichende Sichtweisen.
- In einer Variante müssen alle anderen Funktionswerte höher als der Tiefpunkt sein.
- Eine konstante Funktion (waagrechter Graph) hätte demnach keinen Tiefpunkt.
- In einer anderen Varianten dürfen sie gleich niedrig aber nicht höher sein.[1]
- Dann wären alle Punkte einer kostanten Funktion auch Tiefpunkte.
- Wo die Unterscheidung wichtig ist, muss man gegebenenfalls nachfragen.
Was sind "Tiefwerte" und "Tiefstellen"?
- Das Wort Tiefwert meint nur den y-Wert von einem Tiefpunkt.
- Ein anderes Wort für den Tiefwert ist auch Minimum.
- Das Wort Tiefstelle meint nur den x-Wert von einem Tiefpunkt.
- Beides zusammen ist der Tiefpunkt.
Ist ein Minimum ein Tiefpunkt?
- Nein, als Minimum bezeichnet man nur den y-Wert eines Tiefpunktes.
- Der Tiefpunkt aber hat immer einen x- und einen y-Wert zusammen.
- Siehe auch Minimum ↗
Wie bestimmt man Tiefpunkte?
- Dazu gibt es mehrere Möglichkeiten.
- Man kann sie an einem Graphen ablesen.
- Man kann sie durch Raten herausbekommen.
- Man kann sie rechnerisch bestimmen.
- Mehr unter Tiefpunkte bestimmen. (externer Link)
Was ist eine epsilon-Umgebung?
- Es gibt eine mathematisch exakte Definition für einen Tiefpunkt.
- Es ist ein Punkt, in dessen epsilon-Umgebung keine tieferen Punkte liegen.
- Das heißt, wenn man eine beliebig kleine Umgebung links und rechts ...
- von dem Tiefpunkt finden kann, in der alle anderen Werte höher sind, ...
- dann war der untersuchte Punkt auch ein Tiefpunkt.
- Mehr dazu unter epsilon-Umgebung ↗
Synonyme
Fußnoten
- [1] Der Tiefpunkt (Extremum) als Punkt der gleich tiefer oder tiefer den anderen Punkten ist wird zum Beispiel so definiert in: Guido Walz: Spektrum Lexikon der Mathematik. Band 2: Eig bis Inn; 2001; ISBN: 3-8274-0437-7