Hochpunkt
Analysis
Basiswissen
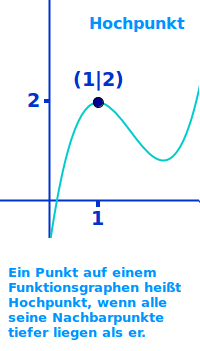
Hoch- und Tiefpunkte fasst man zu den Extrempunkten zusammen: in der Schulmathematik ist ein Hochpunkt der höchste Punkt eines hügelartigen Stückes eines Graphen. Das wird hier kurz erklärt. Ergänzend wird auch die korrekte mathematische Definition gegeben.
Schulmathematische Handhabung
Bei einer nach unten geöffneten Parabel ist der Scheitelpunkt gleichzeitig auch der höchste Punkt der Parabel. Ist ein solcher Hochpunkt Teil eines Graphen, der weder Lücke noch Knicke hat, dann kann man ihn über die erste Ableitung f'(x) sowie die zweite Ableitung f''(x) berechnen. Mehr zu Berechnung unter Hochpunkte bestimmen ↗
Was ist die korrekte Definition eines Hochpunktes?
Das Wichtigste zuerst: ein Hochpunkt ist nicht über die ersten zwei Ableitungen definiert. Der Graph einer Funktion kann zum Beispiel aus getrennten Punkten mit Lücken dazwischen bestehen oder es kann eine Zickzackkurve vorliegen. Jeder Punkt in einem betrachteten Bereich, für den es keine höheren Punkte gibt, ist per Definition ein Hochpunkt. Mehr zu dieser Definition unter Extrempunkt ↗
Was bedeuten "Hochstelle" und "Hochwert"?
- Der x-Wert des Hochpunktes ist die Hochstelle ↗
- Der y-Wert des Hochpunktes ist der Hochwert ↗
Was ist ein absoluter Hochpunkt?
Ein Punkt, der in einem fest definierten Bereich keine höheren Punkte hat, gilt für diesen Bereich als absoluter Hochpunkt. Oft ist der betrachtete Bereich der gesamte Definitionsbereich einer Funktion. Mehr unter absoluter Hochpunkt ↗
Was ist ein lokaler Hochpunkt?
Ein Punkt, der nur in seiner Umgebung ein Hochpunkt ist. Jeder Punkt, der höher ist als sein linker und rechter Nachbar ist damit ein Hochpunkt. Mehr unter lokaler Hochpunkt ↗
Fußnoten
- [1] Der Hochpunkt (Extremum) als Punkt der gleich hoch oder höher als andere Punkte: Guido Walz: Spektrum Lexikon der Mathematik. Band 2: Eig bis Inn; 2001; ISBN: 3-8274-0437-7