Gerade
Übersicht
Basiswissen
Eine Gerade in der Mathematik ist eine Linie ohne Ecken, Lücken, Kurven oder Enden: sie ist unendlich lang gedacht. Die kürzeste Verbindung zwischen zwei Punkten liegt immer auf einer Geraden. Hier werden Geraden in verschiedenen Teilgebieten der Mathematik kurz vorgestellt.
Definition einer Geraden in der Geometrie
- In der Mathematik ist eine Gerade eine Linie ohne Anfang und Ende.
- Mathematische Geraden sind also sozusagen unendlich lang gedacht.
- Außerdem werden sie als unendlich dünn gedacht.
- Mathematische Geraden haben keine Dicke.
- Die kürzeste Verbindung zwischen zwei Punkten liegt immer auf einer Geraden.
- Siehe auch Euklidische Geometrie ↗
Definition einer Geraden in der Gleichungslehre
- y = mx+b:
- Eine Gleichung wie x+y=10 hat unendlich viele Lösungen.
- Man kann die Lösungen in einem 2D-Koordinatensystem darstellen.
- Dann ergeben alle Lösungen zusammen gedacht eine Gerade.
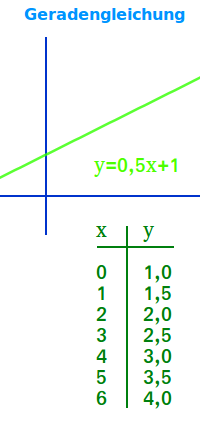
- Eine solche Gerade heißt Geradengleichung ↗
Definition einer Geraden als Funktionsgraph
- f(x) = mx + b:
- Es gibt auch lineare Funktionen, wie f(x)=2x-4.
- Für jede Zahl, die man für x einsetzt, kann man einen y-Wert ausrechnen.
- Die x-y-Pärchen kann man als Koordinaten von Punkten auffassen.
- Alle möglichen Punkte geben dann wieder eine Gerade.
- Mehr dazu unter lineare Funktion ↗
Definition einer Geraden in der Vektorrechnung
- Vektorrechnung meint hier dasselbe wie analytische Geomtrie oder lineare Algebra.
- In diesem Gebiet der Mathematik geht es um Geraden im 3D-Raum.
- Mehr dazu unter 3D-Gerade ↗
Geraden in der Geometrie
- In der Geometrie meint gerade soviel wie ohne Ecken, Kurven oder Lücken.
- Eine gerade Linie ist dann immer der kürzeste Weg zwischen zwei Punkten.
- Man unterscheidet z. B. Strahlen, Halbgeraden oder Strecken.
- Mehr dazu unter Geraden ↗
Eine Zahl als gerade Zahl
- Man spricht von geraden Zahlen. Die 0, 2, 4 oder 18 sind gerade.
- Eine Zahl heißt gerade, wenn sie ohne Rest durch zwei teilbar ist.
- Mehr dazu unter gerade Zahl ↗
Heißt geradeaus immer auch gerade?
Das Wort gerade steckt als Bestandteil in vielen anderen Worten, zum Beispiel geradeaus, geradlinig, geradewegs oder kerzengerade. Das was man im Alltag aber unter geradeaus oder geradlinig versteht, kann zum Teil deutlich von dem abweichen, was man darunter in der Geometrie versteht. Wenn man zum Beispiel sagt, dass ein Eisenbahnlinie kerzengerade immer nur geradeaus durch eine Wüste führt, dann verläuft die Eisenbahnlinie nicht auf einer geometrischen Gerade. Das ist näher erklärt im Artikel zum Adjektiv geradeaus ↗