Sekantenverfahren
Methode zum Bestimmen der Steigung in einem Punkt
Basiswissen
Das Sekantenverfahren, auch h-Methode genannt, ist die grundlegende Methode zur Bestimmung der Steigung eines Graphen in einem bestimmten Punkt. Bei Sachaufgaben ist das Ergebnis oft die momentane Änderungsrate. Das Verfahren wird hier in allgemeiner Form Schritt für Schritt erklärt.
Zweck
Das Sekantenverfahren, auch h-Methode genannt, dient dazu, die Steigung eines Funktionsgraphen an genau einem einzigen Punkt zu bestimmen. Der Term dazu heißt Differentialquotient. Das Zahlenergebnis des Verfahrens heißt je nach Kontext Steigung in einem Punkt (geometrisch), momentane Änderungsrate (Sachaufgaben), Tangentensteigung oder erste Ableitung (innermathematisch). Siehe dazu auch Steigung in einem Punkt ↗
Steigungsdreieck
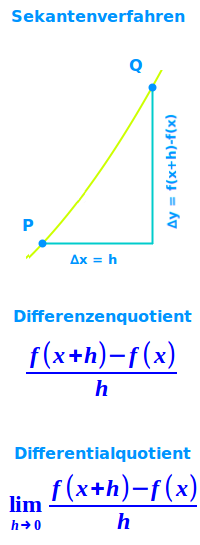
Man hat einen beliebigen Punkt P auf einem Funktionsgraphen. Für diesen Punkt soll die Steigung der Tangente bestimmt werden. Man wählt dazu zusätzlich zu P noch einen zweiten Punkt Q in der Nähe von P aus. Für die beiden Punkte erstellt man ein Steigungsdreieck. Grundlagen dazu unter Steigungsdreieck aus Graph ↗
Sekantensteigung
Über das Steigungsdreieck kann man einen Term für die mittlere Steigung zwischen diesen zwei Punkten angeben. Dieser Term steht für die Sekantensteigung (Gerade durch P und Q). Mehr dazu unter Sekantensteigung ↗
Tangentensteigung
Man baut dann in diesem Term eine Variable ein, die den Abstand zwischen den beiden Punkten angibt (oft ein kleines h). Für diese Variable bildet man dann den Grenzwert gegen 0. Anschaulich meint das: die zwei Punkte nähern sich beliebig weit aneinander an. Der Grenzwert gibt eine exakte Zahl. Diese Zahl ist die Steigung der Tangente oder auch die Steigung des Graphen in genau dem Punkt P. Der entsprechende Term heißt auch Differentialquotient ↗