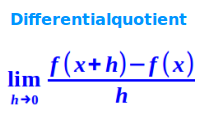Differentialquotient
dy/dx
Basiswissen
Der Begriff spielt eine Rolle bei der Bestimmung der Tangententsteigung beziehungsweise der ersten Ableitung einer Funktion. Er wird hergeleitet aus einem Steigungsdreieck.
Bildung
Aus einem Steigungsdreieck zwischen zwei Punkten wird zunächst ein Term für die mittlere Steigung zwischen diesen zwei Punkten aufgestellt. Dieser Term ist der Differenzenquotient ∆y/∆x. Indem man die Breite ∆x des Steigungsdreiecks immer weiter gegen 0 laufen lässt, wird aus der mittleren Steigung immer mehr die wahre Steigung an einem Punkt. Der Term für die Steigung nach der Grenzwertbildung liefert dann die Steigung in einem Punkt. Dieser Term ist der Differentialquotient dy/dx. "Differential" deutet an, dass für die ursprünglichen Differenzen der Grenzwert gegen 0 gebildet wurde. Mehr zum Verfahren unter Sekantenverfahren ↗
∆y/∆x
- Das ∆ ist ein großes griechisches Delta
- Der ganze Term heißt Differenzenquotient.
- Er steht für die mittlere Steigung zwischen zwei Punkten.
- Die Grenzwertbildung hat noch nicht stattgefunden.
dy/dx
- Das ist der Differentialquotient.
- Er steht für die momentane Steigung in einem Punkt.
- Die Grenzwertbildung dx ⭢ 0 hat stattgefunden.
- Der Ausdruck ist sinngleich mit f'(x).
f'(x)
- Man hat eine Funktion: f(x)
- Man kann dann den Differentialquotienten bilden.
- Macht man das nicht für eine bestimmte x-Stelle wie x=3, sondern ...
- lässt man x als Variable offen, dann kann man am Ende x-Werte einsetzen.
- Der x-Wert eingesetzt in den Differentialquotienten gibt dann die Steigung.
- Man hat also eine eindeutige Zuordnung: für jeden x-Wert gibt es eine Steigung.
- Der Differentialquotient mit variablem x kann dann als Funktion geschrieben werden.
- Die übliche Abkürzung f'(x) und heißt erste Ableitung ↗
Fußnoten
- [1] Ein Lexikon des Jahre 1857 verwendet ausführlich die heute übliche Schreib- und Sprechweisen: "Differentialrechnung. Die Differenz einer Function y = f(x) ist ∆y = f(x + ∆x) – f(x), s. Differenz. Wenn nun die Function y in der Nähe von x, welches als irgend ein bestimmter Werth der unabhängigen Veränderlichen betrachtet wird, stetig ist u. in diesem Falle daher einen reellen Werth hat, so nähert sich, wenn sich ∆x der Null nähert, der Quotient einer bestimmten endlichen Grenze bis zu jedem beliebigen Grade." Der Artikel geht noch lange und ausführlich weiter. In: Pierer's Universal-Lexikon, Band 5. Altenburg 1858, S. 146-147. Online: http://www.zeno.org/nid/20009786759