Steigungsdreieck
Dreieck zur anschaulichen Bestimmung der Steigung
Wofür gibt es Steigungsdreiecke?
◦ Steigungsdreiecke gehören immer zu Graphen.
◦ Eine Gerade in einem Koordinatensystem nennt man zum Beispiel Graph.
◦ Auch Parabeln oder Hyperbeln in Koordinatensystemen nennt man Graph.
◦ Graphen gehören oft zu Gleichungen, oft von Funktionen.
◦ Für jeden Graphen kann man Steigungsdreiecke zeichnen.
Was ist ein Steigungsdreieck?
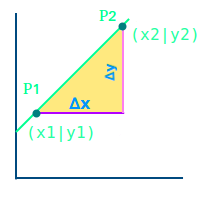
◦ Ein Dreieck, dessen längste Seite durch zwei Punkt auf dem Graphen geht.
◦ (Welche Punkte von dem Graphen man dafür nimmt, ist egal.)
◦ Den linken Punkt nennt man oft P1 mit den Koordinaten (X1|Y1).
◦ Den rechten Punkt nennt man oft P2 mit den Koordinaten (X2|Y2).
◦ Eine der kürzeren Seiten von dem Dreieck verläuft waagrecht (parallel zur x-Achse).
◦ Die andere der zwei kürzen Seiten verläuft senkrecht (parallel zur y-Achse).
Woher kommt der Name?
◦ Bei Graphen spricht man oft von Steigung.
◦ Die Steigung sagt, wie steil ein Graph bei einem bestimmten Punkt ist.
◦ Bei einer Steigung von 0 verläuft der Graph "flach" von links nach rechts.
◦ Spielplatzrutschen haben Steigungen von etwa 0,6 bis höchstens etwa 1,7.
◦ Mit dem Steigungsdreieck kann man diese Steigung von einem Graphen leicht bestimmen.
◦ Man teilt einfach nur die senkrechte Höhe des Dreiecks durch seine waagrechte Breite.
◦ Was dabei herauskommt ist die Steigung des Graphen in der Gegend von dem Steigungsdreieck.
Welche Fachworte gibt es?
◦ Die Länge der waagrechten Seite heißt ∆Y, mehr unter => Delta x
◦ Die Länge der senkrechten Seie heißt ∆X, mehr unter => Delta y
Siehe auch
=> Lineare Funktionen [Übersicht]
=> Steigungsdreieck aus Graph [zeichnen]
=> Steigungsdreieck aus Geradengleichung [zeichnen]
=> Steigungswinkel aus Steigungsdreieck
=> Steigung aus Steigungsdreieck
=> Steigung aus zwei Punkten [formal]
=> Steigung [was sie bedeutet]
=> Steigungen [Beispielwerte]
=> Differenzenquotient
