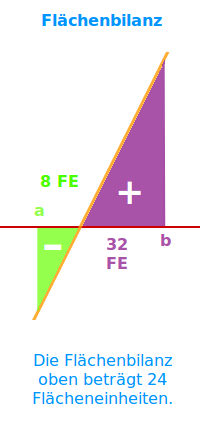
Flächenbilanz
Integralrechnung
Definition
Als Flächenbilanz bezeichnet man bei Funktionsgraphen das Ergebnis einer gegenseitigen Verrechnung von Flächen unter- und oberhalb der x-Achse. Flächen unterhalb der x-Achse verringern dabei das Endergebnis: Hat ein Graph in einem bestimmen Bereich (Intervall) 5 FE (Flächeneinheiten) unter der x-Achse und 6 FE über der x-Achse, dann ist seine Flächenbilanz 1 FE. Das + und das - heben sich also aus gegenseitig aus.
Was muss gegeben sein?
- Man hat eine Funktion f(x) mit einem Graphen.
- Man betrachtet ein Intervall von a bis b.
- a ist die linke Integrationsgrenze ↗
- b ist die rechte Integrationsgrenze ↗
- Zwischen a und b darf es eine oder auch mehrere Nullstellen geben.
- Es muss aber keine Nullstelle im Intervall a bis b vorhanden sein.
Wie wird die Flächenbilanz berechnet?
- Die Flächenbilanz berechnet man immer zwischen zwei Grenzen a und b.
- Die Flächenbilanz ist gleich dem bestimmten Integral von a bis b.
- Man bildet erst die Stammfunktion F(x) und rechnet dann: F(b)-F(a)
- Das Ergebnis ist dann immer der Wert der Flächenbilanz.
- Siehe auch bestimmtes Integral berechnen ↗
Wie bestimmt man die Flächenbilanz graphisch?
- Man geht dabei überschlägig vor:
- Man schätzt Teilflächen am Funktionsgraph ab.
- Was über der x-Achse liegt wird addiert.
- Was unter der x-Achse liegt, wird subtrahiert.
- Das Ergebnis kann negativ, positiv oder auch 0 sein.
- Lies mehr unter anschaulich integrieren ↗
Wie lässt sich die Flächenbilanz deuten?
- Von a bis b verläuft der Graph teilweise über und teilweise unter der x-Achse.
- Man betrachtet alle Teilflächen und addiert sie gedanklich zusammen.
- Dabei rechnet man Flächen unter der x-Achse als negative Zahl.
- Flächen oberhalb der x-Achse rechnet man als positive Zahl.
- Die Summe aus negativen und positiven Werten ist die Flächenbilanz.
- Die Flächenbilanz kann positiv, negativ oder auch 0 sein.
Was wäre ein Beispiel?
- f(x)=x-3
- Mit a = 0 und b = 3:
- Das ist eine Normalgerade, die um 3 nach unten geschoben ist.
- Eine Nullstelle hat sie bei x=3.
- Von 0 bis 3 liegt die Fläche unter der Kurve.
- Der orientierte Flächeninhalt ist -4,5.
- (Die absolute Fläche bzw. der Flächenbetrag wäre 4,5.)
- Von 3 bis 7 ist die Fläche dann ganz über der x-Achse.
- Die orientierte Fläche von 3 bis 7 ist dann 8.
- Die Flächenbilanz von 0 bis 8 wäre dann -4,5 plus 8, also: 3,5 ✔