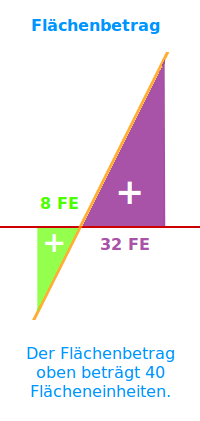
Flächenbetrag
Alle Teilflächen sind +
Basiswissen
In der Integralrechnung ist der Flächenbetrag die Summe aller positiv gerechneten Teilflächen, die ein Funktionsgraph mit der x-Achse bildet. Flächen unterhalb der x-Achse werden dabei auch positiv (+) gerechnet. Der Flächenbetrag kann nie negativ sein. Er ist entweder 0 oder eine positive Zahl.
Fläche
Das Wort Flächenbetrag kommt vor allem in der Integralrechnung vor. In der Integralrechnung will man oft berechnen, wie groß die Fläche zwischen einer Funktionskurve und der x-Achse ist. Ganz egal, ob die Kurve nun oberhalb oder unterhalb der x-Achse liegt, spricht man immer von der Fläche unter der Kurve.
Definition
- Beim Flächenbetrag werden alle Flächen positiv gerechnet.
- Egal ober unter oder über der x-Achse: Flächen kriegen immer ein +.
- Der Flächenbetrag ist immer die Summe von absoluten Flächen.
- Absolut meint: nie mit minus, immer nur mit plus
Zahlenbeispiel
- f(x) = 2x
- Von -2 bis 0 liegt die Fläche unter der Kurve unter der x-Achse.
- Troztdem hat sie ein positives Vorzeichen, man hat 8 Flächeneinheiten.
- Von 0 bis 4 liegt die Fläche über der x-Achse.
- Ihre Größe ist 32 Flächeneinheiten.
- Beides zusammen gibt 40 FE.
- Das ist der Flächenbetrag.
Berechnung
- In der Integralrechnung erhält man Flächen über ein sogenanntes bestimmtes Integral ↗
- Das bestimmte Integral gibt Flächen unter der x-Achse automatisch ein Minus.
- Würde man im Beispiel oben von -2 bis 4 integrieren, käme 24 heraus.
- Das wäre nicht der Fächenbetrag, sondern die Flächenbilanz ↗
- Den Flächenbetrag muss man abschnittsweise berechnen.
- Man integriert von Nullstelle zu Nullstelle.
- Negative Teilflächen setzt man dann positiv.
- Dann erst die positiven Beträge addieren.
Was ist das Gegenteil?
- Eine Art Gegenteilt ist die orientierte Fläche.
- Statt orientierter Fläche sagt man auch Flächenbilanz.
- Hier werden Teilstücke unterhalb der x-Achse negativ gerechnet.
- + und - Flächenstücke können sich also gegenseitig ausgleichen.
- Mehr dazu unter Flächenbilanz ↗