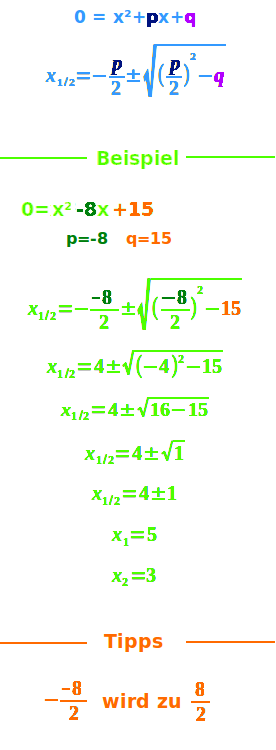pq-Formel
Übersicht
Basiswissen
- p/2 ± √((p/2)²-q) ist die Standardformel zum Lösen einer quadratischen Gleichung. Die Gleichung muss dabei in der sogenannten Normalform gegeben sein: 0 = x² + px + q. Das ist näher erklärt.
Schreibweisen für die pq-Formel
- x = -p/2 ± Wurzel aus [(p/2)²-q]
- x = -p/2 ± √[(p/2)²-q]
Wann kann man die pq-Formel nutzen?
- Die pq-Formel gilt nur für eine quadratische Gleichung ↗
- Mit der pq-Formel kann man jede quadratische Gleichung lösen.
- Man braucht immer die Normalform der quadratischen Gleichung ↗
- Das wird hier jetzt näher erklärt.
MERKSATZ 1.0: Die pq-Formel kann man immer zum Lösen von quadratischen Gleichungen benutzen. Man kann sie aber auch nur zum Lösen von quadratischen Gleichungen nutzen. ✓
1. Schritt: Normalform prüfen
- 0 = x² + px + q
- Links vom Gleichzeichen darf nur 0 stehen.
- Rechts kommt zuerst das x² ohne irgendetwas davor.
- Dann darf ein + oder - mit einer Zahl und einem x danach kommen.
- Am Ende darf ein + oder - mit einer Zahl ohne x kommen.
- Normalform nicht OK: 4=x²-8x+16 | links keine 0
- Normalform nicht OK: 0=2x²-8x+16 | 2 vor dem x²
- Normalform nicht OK: 0=-x²-8x+16 | - vor dem x²
- Normalform OK: 0=x²-8x+16 ✔
- Normalform OK: 0=x²+4x+0 ✔
- Normalform OK: 0=x²+0x+4 ✔
- Normalform OK: 0=x²+0x+0 ✔
MERKSATZ 2.0: Die pq-Formel kann man nur verwenden, wenn man die quadratische Gleichung in der Normalform 0 = x²+px+q gegeben hat. Vor dem x² darf nichts mehr stehen. ✓
2. Schritt: Normalform herstellen
- Falls man noch nicht die Normalform hat, ...
- dann muss man sie durch Umformen herstellen.
- Siehe unter Normalform für pq-Formel herstellen ↗
3. Schritt p und q festlegen
- Man hat die Normalform: 0 = x² - 8x + 15
- p und q aus der Normalform ablesen:
- Das p ist der Faktor (Zahl) vor dem x.
- Achtung: das Vorzeichen gehört dazu.
- Im Beispiel ist das p die Zahl -8.
- Das q ist die alleinstehende Zahl ohne x.
- Im Beispiel ist das p die +15
MERKSATZ 3.0: Die Vorzeichen gehören zum p und zum q. Bei 0 = x²-8x+15 ist p=-8 und q=8. ✓
Tipp
- Ein Vorzeichen gehört immer mit zur Zahl.
- Wenn vor dem x keine Zahl steht, dann ist p=1.
Sonderfall: das p fehlt
- Wenn es gar kein x ohne Quadrat gibt, dann ist p=0.
- Beispiel: 0 = x² + 16 ⭢ p = 0
Sonderfall: das q fehlt
- Wenn es am Ende keine Zahl für q gibt, dann ist q=0.
- Beispiele: 0 = x² - 4x ⭢ q = 0
MERKSATZ 4.0: Fehlt das Glied nur mit, so ist p=0. Fehlt das Glied ganz ohne x (nur Zahl), dann ist q=0. ✓
4. Schritt: p und q in Formel einsetzen
- Setze die Zahlen von oben für p und q ein:
- Erste Nullstelle: x₁ = -p/2 + Wurzel aus [(p/2)² - q]
- Zweite Nullstelle: x₂ = -p/2 - Wurzel aus [(p/2)² - q]
Tipp: wie viele Lösungen es geben kann
- Der Term unter der Wurzel heißt Diskriminante.
- Ist die Diskriminante kleiner als Null, dann gibt es keine Lösungen.
- Ist die Diskriminante genau gleich Null, dann gibt es genau eine Lösung.
- ist die Diskriminante größer als Null, dann gibt es zwei Lösungen.
- Mehr unter Diskriminante bei pq-Formel ↗
Beispiel I
0 = x² -8x + 15
p = -8
q = 15
x₁ = 5 ✔
x₂ = 3 ✔
Beispiel II
0 = x² + 4x
p = 4
q = 0
x₁ = -4 ✔
x₂ = 0 ✔
Beispiel III
0 = x² - 16
p = 0
q = -16
x₁ = -4 ✔
x₂ = 4 ✔
Aufgaben dazu
Aufgaben zur pq-Formel sind hier als Quickcheck zusammengestellt. Zu jeder Aufgabe gibt es immer auch eine Lösung. Direkt zu den Aufgaben geht es über => qck