Wahrscheinlichkeitsdichte
Stochastik
Basiswissen
Hat ein Zufallsexperiment potentiell unendlich viele Ergebnismöglichkeiten tritt ein Problem auf: ordnet man jedem Ergebnis eine Wahrscheinlichkeit zu, kan die Summe aller Wahrscheinlichkeiten größer als 1 werden. Das aber ist theoretisch unmöglich. Die Lösung ist die Wahrscheinlichkeitsdichte. Das ist hier erklärt.
Kein Problem: diskrete Ergebnisse
Würfelt man mit einem Spielwürfel, kann es insgesamt 6 verschiedene Ergebnisse geben: die Zahlen 1 bis 6. Jeder Zahl kann man eine Wahrscheinlichkeit zuordnen, dass sie erscheint. Bei einem fairen Würfel hätte jede Zahl die Wahrscheinlichkeit 1/6. Die Summe aller möglichen Wahrscheinlichkeiten (sicheres Ereignis) muss dabei immer genau 1 ergeben. Das ist hier auch der Fall.
Problematisch: stetige Ergebnisse
Als Beispiel betrachten wir die Wahrscheinlichkeit, dass sich ein Elektron an einem bestimmten Ort in einem Atom aufhält. Ein Ort kann als Punkt im Raum mit drei Koordinaten x, y und z angegeben werden. Es erscheint logisch, dass man für x, y und z beliebige reelle Zahlen einsetzen kann. Das heißt in Konsequenz, dass es theoretisch unendlich viel Punkte gibt, für die man nach einer Wahrscheinlichkeit fragen kann. Ordnet man jedem mathematisch möglichen Punkt in einem Atom eine Wahrscheinlichkeit zu, dann erhält man unendlich viele solche Angaben. Die Summe alle dieser Wahrscheinlichkeiten könnte dann aber über 1 liegen. Dies ist aus theoretischen Gründen aber unmöglich. Hat man unendlich viele Ergebnismöglichkeiten, kann dieses Problem auftreten.
Die Lösung: Wahrscheinlichkeitsdichte
Der Grundgedanke der Wahrscheinlichkeitsdichte ist: man erlaubt nicht mehr danach zu fragen, welche Wahrscheinlichkeit für einen konkreten Zahlenwert oder einen bestimmten Ort im Raum besteht. Stattdessen erlaubt man nur die Frage nach Wahrscheinlichkeiten für bestimmten Bereiche, Intervalle oder Raumelemente: wie groß ist die Wahrscheinlichkeit, dass ein Elektron in einem bestimmten Raumbereich vorhanden ist? Damit kann sichergestellt werden, dass die Wahrscheinlichkeit für alle möglichen Ergebnisse immer genau 1 ergibt.
Berechnung konkreter Wahrscheinlichkeiten
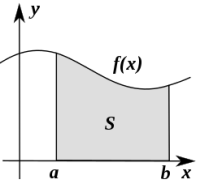
Mit einer Wahrscheinlichkeitsdichte kann man nur Wahrscheinlichkeiten von-bis, also in einem Bereich oder Intervall berechnen. Diese Wahrscheinlichkeit ist dann gleich dem Inhalt der Fläche unter der Kurve von der Zahl a bis zur Zahl b. Die Berechnung erfolgt meist als Integral. Mathematisch benutztman dazu die sogenannte Wahrscheinlichkeitsdichtefunktion ↗
Fußnoten
- [1] Walter R. Fuchs: Titel: Moderne Physik. Manfred Pawlak Verlagsgesellschaft mbH, Herrsching. Erstauflage 1965 oder früher. Dort Seite 183.