Vektor orthogonal zu zwei anderen über LGS
Beispielrechnung
Basiswissen
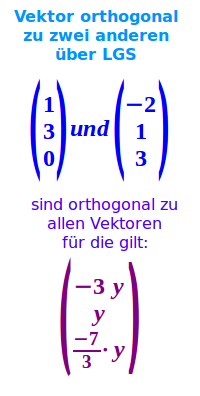
LGS meint hier: Lineares Gleichungssystem. Gegeben sind zwei Vektoren. Die Vektorkoordinaten des einen Vektors a sind zum Beispiel 1, 3 und 0. Die Koordinaten des anderen Vektors b sind -2, 1 und 3. Gesucht sind alle Vektoren, die senkrechten auf jeweils beiden gegebenen Vektoren stehen.
Schritt 1
LGS aufstellen: Gesucht ist ein unbekannter Vektor mit den Komponenten x, y und z. Diesen Vektor kann man einmal mit dem ersten gegebenen Vektor skalar multiplizieren und das Ergebnis gleich Null setzen. Dann multipliziert man den unbekannten Vektor noch mit dem zweiten gegebenen Vektor und setzt das Ergebnis gleich Null. Dadurch entsteht ein lineares Gleichungssystem:
- +1x + 3y + 0z = 0
- -2x + 1y + 3z = 0
Dieses Gleichungssystem hat mehr Unbekannte (x, y und z) als Gleichungen. Solche Gleichungssysteme nennt man auch unterbestimmt. Was das für die Lösung bedeutet ist im Folgenden erklärt.
Schritt 2
LGS deuten: Bei unterbestimmten Gleichungssystemen kommen oft keine eindeutigen sondern mehrdeutige Lösungen heraus. Das heißt, es wird gleich auf irgendeine Weise mehrere Lösungen für das LGS geben, die dann aber alle richtig sind. Geometrisch lässt sich das so deuten, dass es unendlich viele Vektoren gibt, die sowohl senkrecht auf dem Ausgangsvektor a wie auch senkrecht auf dem Ausgangsvektor b stehen. Zum einen unterscheiden sich die Vektoren in ihrer Länge. Zum anderen in ihrer Orientierung. Das muss gleich irgendwie beim Lösen des LGS deutlich werden, was wiederum mit der Unterbestimmtheit zusammen hängt.
Schritt 3
LGS lösen: Man kann das LGS über den Gauß-Algorithmus, das Additions- Gleichsetzungs- oder Einsetzungsverfahren lösen. Alle Verfahren führen zum selben Ergebnis. Hier wird das Einsetzungsverfahren gewählt. Die erste Gleichung kann umgeformt werden in x=-3y. Dieser Term für x kann in die zweite Gleichung eingesetzt werden. Man erhält dadurch: -2·(-3y)+1y+3z=0. Umformen ergibt: 7y+3z=0 oder z=(-7/3)·y. Da das LGS unterbestimmt ist, gibt es keine Möglichkeit die Werte näher mit Zahlen zu bestimmen. Das bestmögliche Ergebnis ist:
- x=-3·y
- z=(-7/3)·y
Die Grundidee ist es, dass man je eine Gleichung für zwei verschiedene der gesuchten Unbekannten erhält. Auf den rechten Seiten der beiden Gleichung taucht dann als Unbekannte ausschließlich die dritte Unbekannte auf.
Schritt 4
Lösung deuten: Solange man die zwei Lösungsbedingungen einhält und damit einen Vektor konstruiert, wird dieser senkrecht auf a und b stehen. Man kann also für die Vektorkomponenten y zunächst irgendeinen beliebigen Wert annehmen. Zum Beispiel: y=3. Das setzt man in die beiden Lösungsgleichungen ein und erhält: x=-9 und z=-7. Einer der Lösungsvektoren hätte also die Komponenten: -9, 3 und -7.
Schritt 5
Stichprobe: Man macht mit dem gefundenen Beispielvektor eine Stichprobe: Skalar multipliziert mit a ergibt er tatsächlich 0. Und auch skalar multipliziert mit b ergibt er 0.
Schritt 6
Allgemeine Formulierung: Die Lösung aus Schritt 3 kann man in Worten so formulieren: Egal welchen Wert man für y einsetzt, solange man dann für x das minus-3-fache von diesem y-Wert wählt und für z das minus-7-drittel-fache, solange wird der dadurch entstandene Vektor senkrecht auf den zwei gegebenen Ausgangsvektoren stehen. Allgemein formuliert man dann die drei Komponenten des Ergebnisvektors so: -3y | y | (-7/3)·y
Tipp
Dieser Lösungsweg funktioniert immer, kann aber unter Umständen rechenaufwändig werden. Eine alternative Methode verwendet das Kreuzprodukt der zwei gegebenen Vektoren. Mehr dazu unter Kreuzprodukt ↗