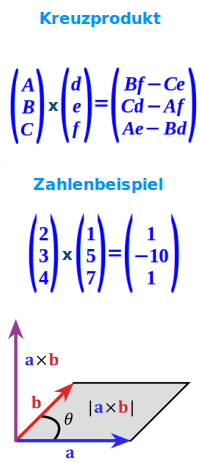
Kreuzprodukt
Vektorrechnung
Basiswissen
Das Kreuzprodukt, auch Vektorprodukt genannt, multipliziert zwei Vektoren so, dass als Ergebnis ein dritter Vektor entsteht. Als Multiplikationszeichen wird nur ein kleines Kreuz verwendet, daher der Name.
Wozu verwendet man das Kreuzprodukt?
Man kann zwei Vektoren so multiplizieren, dass wieder ein Vektor dabei herauskommt. Diesen Vektor nennt man das Kreuzprodukt. Dieser neue Vektor, das Ergebnis, steht immer senkrecht auf beiden Ausgangsvektoren.
Schreibweise
- Korrekt: a×b
- Falsch: a·b
Das Kreuzprodukt berechnen
- 3D-Vektoren haben drei Koordinaten.
- Der erste Vektor habe die Koordinaten (A;B;C).
- Der zweite Vektor habe die Koordinaten (d;e;f).
- Dann ist die oberste Koordinaten des Kreuzproduktes: Bf-Ce
- Die mittlere Koordinate des Kreuzproduktes ist: Cd-Af
- Die untere Koordinate des Kreuzproduktes ist: Ae-Bd
- Siehe auch Kreuzprodukt berechnen ↗
Nicht Kommutativ
- Die Kreuzmultiplikation ist nicht kommutativ.
- a×b gibt etwas anderes als b×a.
- Zwar bleibt die Länge des Ergebnisvektors gleich,
- aber das Ergebnis zeigt in die entgegengesetzte Richtung.
Rechtssystem
- Die zwei Ausgangsvektoren und ihr Kreuzprodukt sind ein Rechtssystem ↗
Das Kreuzprodukt als senkrechter Vektor
- Das Kreuzprodukt c von zwei Vektoren a und b steht immer senkrecht auf diesen beiden Vektoren a und b.
- Man sagt auch, der Ergebnisvektor ist orthogonal zu beiden Ausgangsvektoren. Siehe auch orthogonale Vektoren ↗
- Das heißt: Das Kreuzprodukt c steht sowohl senkrecht auf dem Ausgangsvektor wie auch auf dem Ausgangsvektor b.