Nullstellen von kubischen Funktionen über Faktorisieren
Übersicht
Basiswissen
f(x) = x³-x² kann man faktorisieren und erhält dann f(x) = x²·(x¹-1). Für diese umgeformte Variante kann man drei Nullstellen direkt ablesen: 0, -1 und 1. Das Lösungsverfahren ist hier erklärt.
Was meint faktorisieren?
- Ein Faktor ist ein Teil einer Malkette.
- Faktorisieren heißt, dass man einen Term in eine Malkette umwandelt.
- Der erste Schritt bei diesem Verfahren ist oft das Ausklammern.
- Manchmal muss man auch die 3. binomische Formel verwenden.
- Aus Malketten kann man leicht die Nullstellen ablesen.
- Mehr unter Satz vom Nullprodukt ↗
Wann ist die Methode erfolgreich?
- Das geht oft gut mit kubischen Funktionen ohne absolutes Glied.
- Was das meint steht unter Absolutes Glied einer kubischen Funktion ↗
- Das absolute Glied ist der Teil im Funktionsterm "ohne x":
- Beispiel a: f(x)=x³+4x²+x ⭢ faktorisierbar
- Beispiel b: f(x)=4x³-x ⭢ faktorisierbar
- Beispiel c: f(x)=4x³-9 ⭢ nicht faktorisierbar
- Beispiel d: f(x)=x³+x²+1 ⭢ nicht faktorisierbar
1. Schritt
- Ausklammern:
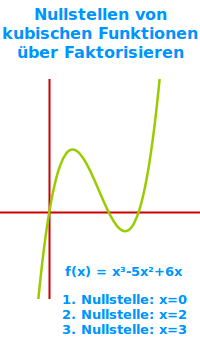
- Gegeben ist zum Beispiel: f(x) = x³-5x²+6x
- Man klammert das x einmal aus, das gibt:
- f(x) = x·[x²-5x+6]
2. Schritt
- Erste Lösung hinschreiben.
- Nach dem Ausklammern steht immer ein x vor der Klammer.
- Das ist die erste von insgesamt drei möglichen Nullstellen.
- Man schreibt: x = 0
3. Schritt
- In der Klammer steht nach dem Ausklammern immer eine quadratische Funktion.
- Im Beispiel oben wäre ihr Funktionsterm: x²-5x+6
- Von dieser sucht man dann alle möglichen Nullstellen.
- Eine Möglichkeit Nullstellen über pq-Formel ↗
- Andere Möglichkeit Nullstellen über ABC-Formel ↗
- Für das Beispiel ergeben sich: x=3 und x=2
- Das sind die zwei weiteren Nullstellen.
- Man schreibt: x=3 oder x=2.
4. Schritt
- Alles Lösungen gemeinsam aufschreiben:
- f(x) hat drei Nullstellen:
- x=0, x=2 und x=3 ✔
Binomische Formel
- Ein Term der Form a²-b² kann direkt faktorisiert werden.
- Es gilt: a²-b² = (a+b)·(a-b)
- Beispiel: 16-x² wird zu (4+x)·(4-x)
- Mehr dazu unter Dritte binomische Formel rückwärts ↗
Aufgaben dazu
Aufgaben zum Üben mit Lösungen sind hier zusammengestellt als Quickcheck. Zu den Aufgaben geht es über => qck