Halbwertszeit
Definition
Basiswissen
Die Zeit, in der sich irgendwas halbiert nennt man die Halbwertszeit, kurz die HWZ. Die übliche Abkürzung ist ein großes lateinisches T. Hier stehen Beispiele.
Was meint Halbwertszeit?
- Es gibt Dinge, die in einer bestimmten Zeit immer um die Hälfte weniger werden.
- Die Zeit die eine Halbierung der Menge braucht nennt man Halbwertszeit.
Was wäre ein Beispiel?
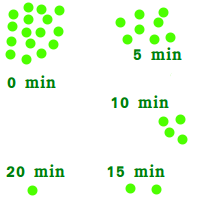
- Angenommen irgendein Element hätte eine Halbwertszeit von 5 Minuten.
- Und angenommen wir hätten am Anfang 16 Atome von diesem Element.
- Dann wären es nach 5 Minuten nur noch etwa 8 Atome.
- Nach weiteren 5 Minuten wären es nur noch 4 Atome.
- Und wieder nach 5 Minuten nur noch 2 Atome.
- Und nach insgesamt 20 Minuten wär es nur 1 Atom.
- Und irgendwann nach weiteren 5 Minuten wäre auch dieses weg.
Wo sind Halbwertszeiten wichtig?
- Halbwertszeiten sind wichtig beim Abbau von Stoffen in Organismen, mehr unter Biologische Halbwertszeit ↗
- Halbwertszeiten sind wichtig beim radioaktiven Zerfall von Atomen, mehr unter Halbwertszeiten von Nukliden ↗
- Halbwertszeiten sind wichtig bei Zitierhäufigkeiten von Büchern, mehr unter Pharmakokinetische Halbwertszeit ↗
- Halbwertszeiten sind wichtig beim Zerfall von Computerpreisen, mehr unter Mooresches Gesetz ↗
Wovon hängt die Halbwertszeit ab?
Von nichts: für jedes radioaktive Element kann man eine Halbwertszeit angeben, die unter allem chemischen und physikalischen Umständen immer gleich ist. Sie hängt zum Beispiel nicht davon ab, in welchen chemischen Verbindungen ein radioaktives Element vorkommt[1] oder wie stark die Neutrinoaktivät der Sonne ist[2] oder sonstigen Umständen. Aus Sicht der Stochastik ist die Wahrscheinlichkeit eines Atoms, in einem bestimmten Zeitraum zu zerfallen eine unbedingte Wahrscheinlichkeit ↗
In welchen Mathe-Themen tritt es auf?
- Halbwertszeiten gehören ins Thema Wachstum und Zerfall ↗
- Halbwertszeiten gehören ins Thema Exponentialfunktion ↗
Welche Formel beschreibt einen Zerfall mit Halbwertszeit?
- Bauplan: f(x) = a·0,5^x
Legende
- f(x) = Bestand nach x Halbierungsschritten
- a = Bestand bei der 0ten Halbierung (also am Anfang)
- 0,5 = Wachstumsfaktor für die Halbierung [ist immer 0,5]
- x = Anzahl von Halbierungen
Wenn die Lebensdauer gesucht ist
- T = τ · ln(2)
- T = ln(2)/λ
Legende zur Lebensdauer
- T = Halbwertszeit
- τ = kleines Tau Lebensdauer ↗
- ln = El-enn natürlicher Logarithmus ↗
- λ = kleines Lambda Zerfallskonstante ↗
Aufgaben zur Halbwertszeit
Aufgaben zur Halbwertszeit sind hier als Quickcheck zusammengestellt. Zu allen Aufgaben gibt es immer auch die Lösung. Direkt zu den Aufgaben geht es über => qck
Fußnoten
- [1] E.B Norman, G.A Rech, E Browne, R.-M Larimer, M.R Dragowsky, Y.D Chan, M.C.P Isaac, R.J McDonald, A.R Smith, Influence of physical and chemical environments on the decay rates of 7Be and 40K. In: Physics Letters B, Volume 519, Issues 1–2, 2001, Pages 15-22, ISSN 0370-2693. Online: https://doi.org/10.1016/S0370-2693(01)01097-8.
- [2] S. Pommé, H. Stroh, T. Altzitzoglou, J. Paepen, R. Van Ammel, K. Kossert, O. Nähle, J.D. Keightley, K.M. Ferreira, L. Verheyen, M. Bruggeman: Is decay constant? In: Applied Radiation and Isotopes, Volume 134, 2018, Pages 6-12. ISSN 0969-8043. Online: https://doi.org/10.1016/j.apradiso.2017.09.002.