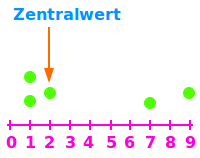
Zentralwert
Statistik
Basiswissen
Der Zentralwert, auch Median genannt, ist die mittlere Zahl in einer aufsteigend sortierten Liste von Zahlen. Bei der Zahlenliste 2;4;7;9;9 ist die 7 die Zahl in der Mitte. Also ist die 7 der Zentralwert. Der Median teilt die Zahlenliste in zwei (ganz oder fast) gleich große Hälften.
Einordnung des Zentralwertes
- Der Begriff gehört in die Statistik ↗
- Zentralwert meint dasselbe wie Median ↗
- Einen Median gibt es aber auch in der Geometrie ↗
- Deshalb nehmen wir für die Statistik das Wort Zentralwert.
- Der Zentralwert ist einer von mehreren Mittelwert[en] ↗
- Der Zentralwert ist eines von mehreren Lagemaße[n]
- Der Zentralwert gehört immer zur einer Liste von Zahlen.
Bedeutung des Zentralwertes
- Der Zentralwert teilt eine Liste von Zahlen in zwei Hälften.
- Die Zahlen der einen Hälfte sind nicht größer als der Zentralwert.
- Die Zahlen der anderen Hälfte sind nicht kleiner als der Zentralwert.
- Jede Zahl, die das leistet, ist ein Zentralwert.
Beispiel 1
- Die Liste hat eine ungerade Anzahl von Zahlen:
- Zahlen von klein nach groß sortieren.
- Dann einfach: Zahl in der Mitte nehmen.
- Man hat die Liste: 2 2 4 5 7 9 12 13 91 91 96
- Die Zahl 9 teilt die Liste in zwei Hälften:
- Die linke Hälfte ist dann: 2 2 4 5 7
- Die rechte Hälfte ist: 12 13 91 91 96
- Jede Hälfte besteht hier aus 5 Zahlen.
- Die 9 ist der Zentralwert der Liste.
- Siehe auch Zentralwert berechnen ↗
Beispiel 2
- Die Liste hat gerade Anzahl von Zahlen:
- Zahlen von klein nach groß sortieren.
- Die zwei Zahlen in der Mitte addieren.
- Davon die Hälfte nehmen:
- Man hat die Liste 4 4 4 6 6 6
- Die Zahl 5 würde die Liste in zwei Hälften teilen:
- Die linke Hälfte wäre 4 4 4
- Die rechte Hälfte wäre 6 6 6
- Die 5 ist der Zentralwert der Liste.
- Siehe auch Zentralwert berechnen ↗