Nabla-Operator
∇
Basiswissen
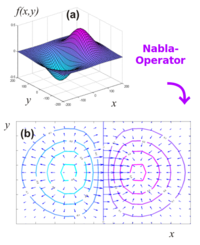
Mit Hilfe des Nabla-Operators wandelt man zum Beispiel ein Skalarfeld (nur Zahlen) in ein Vektorfeld um: die Vektoren zeigen an, in welche Richtung sich die Zahlenwerte am stärksten ändern.
Der Nabla-Operator zur Berechnung des Gradienten eines Skalarfeldes
- Ausgangspunkt ist immer ein gegebenes Skalarfeld ↗
- Der Nabla-Operator macht aus einem Skalarfeld ein Vektorfeld ↗
- Der Vektor wird als Gradient bezeichnet.
- Er gibt an, wie stark sich ein Skalarfeld an einer Stelle ändert.
- Er zeigt in die Richtung der größten Änderung.
- Siehe auch Gradient ↗
Der Nabla-Operator zur Berechnung der Rotation eines Vektorfeldes
- Ausgangspunkt ist ein gegebenenes dreidimensionales Vektorfeld in einem xyz-Koordinatensystem ↗
- Die Rotation ist anschaulich gedeutet die Drehung eines kleines Probekörpers um sich selbst.
- Mit Hilfe des Nabla Operators kann jedem Punkt im Raum die sogenannte Rotation zugeordnet werden.
- Siehe dazu auch Rotation eines Vektorfeldes ↗