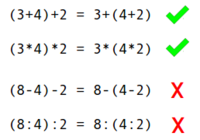Assoziativgesetz
Plus- und Mal: Klammern sind egal
Basiswissen
Das Assoziativgesetzt besagt, dass man bei reinen Plus- und reinen Malaufgaben (Summen, Produkte) Klammern setzen kann wie man will und dass sich dadurch das Rechenergebnis niemals verändern wird.
Aussage des Assoziativgesetzes allgemein
- Aufgaben, bei denen nur plus gerechnet wird heißen Plusketten.
- Aufgaben, bei denen nur mal gerechnet wird heißen Malketten.
- Bei reinen Plus- und bei reinen Malketten sind Klammern egal.
- Man kann Klammern immer setzen, weglassen oder verschieben.
- Egal was man mit den Klammern macht, es kommt immer dasselbe raus.
- Man sagt: Addition (plus) und Multiplikation (mal) sind assoziativ.
Das Assoziativgesetz für die Addition
- Angewandt auf die Addition, kann man sagen:
- Summenden können in beliebiger Reihenfolge zur Teilsummen verbunden werden[1]
- Es gilt also zum Beispiel: 3+(4+5) = (3+4)+5 = (3+5)+4
- Man kann auch sagen: "In einer Summe aus drei oder mehr Zahlen darf man Klammern beleibig setzen oder weglassen. Dabei ändert sich der Wert der Summe nicht."[3]
Das Assoziativgesetz für die Multiplikation
- Angewandt auf die Multiplikation, kann man sagen:
- Faktoren können in beliebiger Reihenfolge zur Teilprodukten verbunden werden[2]
- Es gilt also zum Beispiel: 3·(4·5) = (3·4)·5 = (3·5)·4
- Man kann auch sagen: "In einem Produkt aus drei odre mehr Zahlen darf man Klammern beliebig setzen oder weglassen. Dabei ändert sich der Wert des Produktes nicht."[3]
Was hat das mit dem Kommutativgesetz zu tun?
- Bei Plus- und Malketten macht die Rechenreihenfolge keinen Unterschied am Ergebnis.
- Also kann man die Zahlen vertauschen wie man will (Kommutativgesetz).
- Oder man kann Klammern setzen wie man will (Assoziativgesetz).
- Vertauschen oder Klammern setzen ändert die Rechenreihenfolge.
- Aber das ist bei Plus oder Mal vom Ergebnis her egal.
Beispiel für plus
- 3+4+2 = 9
- (3+4)+2 = 9
- 3+(4+2) = 9
Beispiel für mal
- 3·4·2 = 24
- (3·4)·2 = 24
- 3·(4·2) = 24
Wo gilt das Gesetz nicht?
- Bei der Subtraktion (minus)
- Bei der Division (geteilt)
- Beim Potenzieren (hoch)
- Bei gemischten Plus- und Malketten
- Hier können Klammern einen Unterschied machen.
Name
- Die Klammern verbinden Zahlen miteinander.
- Die verbundenen Zahlen sind rechnerisch enger beieinander.
- Gemeinschaft erzeugen heißt auf Latein assoziieren.
- Daher das Wort Assoziativgesetz
Synonyme
Fußnoten
- [1] Lehr- und Übungsbuch Mathematik. Band I. Verlag Harri Deutsch. Thun und Frankfurt/Main. 20. Auflage. 1989. ISBN: 3 871 44 401 4. Dort heißt es auf Seite 46: "Summanden können in beliebiger Reihenfolge zu Teilsummen verbunden werden". Als Beispiel wird angeführt, dass (a+b)+c = a+(b+c) ist.
- [2] Lehr- und Übungsbuch Mathematik. Band I. Verlag Harri Deutsch. Thun und Frankfurt/Main. 20. Auflage. 1989. ISBN: 3 871 44 401 4. Dort heißt es auf Seite 55: "Faktoren können in beliebiger Reihenfolge zu Teilprodukten verbunden werden". Als Beispiel wird angeführt, dass (2·3)·5 = 2·(3·5) = 3·(2·5) ist.
- [3] Mathematik heute 5. Realschule. Schroedel Diesterweg Verlag. Braunschweig. 2005. ISBN: 3-507-87805-4. Dort auf Seite 92: "In einer Summe aus drei oder mehr Zahlen darf man Klammern beleibig setzen oder weglassen. Dabei ändert sich der Wert der Summe nicht." Sowie: "In einem Produkt aus drei odre mehr Zahlen darf man Klammern beliebig setzen oder weglassen. Dabei ändert sich der Wert des Produktes nicht."