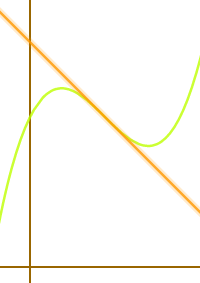
Wendetangente
Definition
Basiswissen
Eine Wendetangente ist eine Gerade, die durch den Wendepunkt einer andere Funktion f(x) geht und die in diesem Punkt genau dieselbe Steigung hat wie die Funktion f(x). Das ist hier näher erklärt.
Was ist eine Wendetangente?
- Eine Wendetangente ist immer eine Gerade.
- Ihre Gleichung kann immer die Form y=mx+b haben.
- Wendetangente meint hier sowohl die Gerade wie auch die Gleichung.
- Eine Wendetangente gehört immer zum Graphen einer anderen Funktion.
- Diese andere Funktion muss einen Wendepunkt haben.
- Die WT berührt den Funktionsgraphen an diesem Punkt.
- Dieser gemeinsame Punkt heißt Berührpunkt ↗
Welche Eigenschaften haben WT?
- Der Graph und die Tangente berühren sich in diesem Berührpunkt.
- Sie hat dort dieselben x- und y-Werte wie dieser Berührpunkt.
- Sie hat dort dieselbe Steigung wie dieser Berührpunkt.
- Man spricht auch von der Wendesteigung ↗
Gibt es Funktionen ohne WT?
- Ja, lineare und quadratische Funktionen z. B. haben keine.
- Kubische Funktionen hingegen haben immer eine Wendetangente.
- Quartische Funktionen können, müssen aber keine WT haben.
Gibt es Funktionen mit mehrere WT?
- Ja, quartische Funktionen (hoch 4) können zwei WT haben.
- Sinus- und Cosinusfunktionen können unendlich viele haben.
Wie bestimmen man WT?
- Erst muss man die Wendepunkte bestimmen.
- Dann legt man dort die Tangente an.
- Wie das geht ist auf einer eigenen Seite erklärt.
- Mehr unter Wendetangenten bestimmen ↗
Fußnoten
- [1] Wendetangente schneidet Kurve, am Beispiel einer Kurve der Geometrie: "Ein Wendepunkt ist dadurch ausgezeichnet, daß die zugehörige Tangente die Kurve in der zweiten Ordnung berührt (s. Kontakt) und im Wendepunkte durch die K. hindurchgeht" In: Meyers Großes Konversations-Lexikon, Band 11. Leipzig 1907, S. 872. Online: http://www.zeno.org/nid/20006959598