Wendetangenten bestimmen
Verfahren
Basiswissen
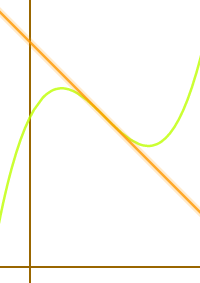
Eine Wendetangente ist eine Gerade, die durch den Wendepunkt einer anderen Funktion geht und genau dan diesem gemeinsamen Punkt dieselbe Steigung wie die andere Funktion f(x) hat. Die Berechnung ist hier ausführlich erklärt.
Definition einer Wendetangente
- Die Wendetangente wird hier t(x) genannt.
- Eine Wendetanente ist immer eine Geradengleichung ↗
- Eine Wendetangente t(x) gehört immer zu einer anderen Funktion f(x).
- Diese andere Funktion f(x) muss immer einen Wendepunkt haben.
- Die Wendetangente t(x) ist dann genau die Gerade,
- die durch den Wendepunkt von f(x) geht und dort ...
- dieselbe Steigung hat wie f(x).
- Siehe auch Tangente ↗
Eigenschaften von Wendetangenten
- t(x) und f(x) haben im Berührpunkt:
- Denselben x-Wert
- Denselben y-Wert
- Dieselbe Steigung
Bestimmung einer Wendetangente
- Allgemeine Form der Geradengleichung: t(x)=mx+b
- Ziel: für t(x)=mx+b für m und b Zahlen finden.
- Wendepunkt von f(x) finden (zweite Ableitung = 0)
- Wie das geht steht unter Wendepunkte bestimmen ↗
- Wendepunkt liegt auch auf der Tangente g(x)...
- Steigung von f(x) in Wendepunkt finden, also f'(x)
- Diese Steigung ist das m von t(x)
- Jetzt kennt man von t(x) einen Punkt und die Steigung.
- Für die Aufstellung einer Geradengleichung gibt es ein festes Verfahren.
- Dazu siehe unter Geradengleichung aus Steigung und Punkt ↗
Vorkommen
- Nicht alle Funktionen haben eine Wendetangente.
- Lineare und quadratische Funktionen z. B. haben keine.
- Kubische Funktionen hingegen haben immer eine Wendetangente.
- Quartische Funktionen können, müssen aber keine WT haben.
Aufgaben dazu
Einige Aufgaben zur Berechnung der Wendetangente sind hier als Quickcheck zusammengestellt. Zu jeder Aufgabe gibt es auch eine Muster-Lösung. Direkt zu den Aufgaben geht es über => qck