Lokales Maximum
Definition
Basiswissen
Der y-Wert oder die Stelle auf der y-Achse, die zu einem lokalen Hochpunkt gehört nennt man ein lokales Minimum. Das ist hier näher erklärt.
Was meint "lokales Maximum"?
- Das Wort bezieht sich auf y-Werte einer Funktion.
- Ein lokales Maximum ist ein y-Wert, dessen direkte Nachbarn kleiner sind.
- Ein lokales Maximum gehört immer zu einem lokalen Hochpunkt ↗
Was wäre ein Beispiel?
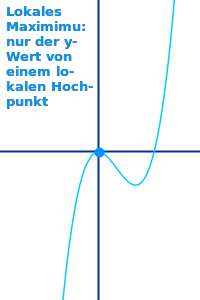
- Betrachte den Graphen von f(x)=x³-3x ↗
- Links gibt es einen Hochpunkt bei x=-1.
- Der y-Wert von diesem Hochpunkt ist 2.
- Direkt links und rechts davon gibt es keine höheren Werte.
- Direkt links und rechts davon sind nämlich alle y-Werte kleiner.
- So einen lokal maximalen y-Wert nennt man lokales Maximum.
- Der entsprechende x-Wert ist die lokale Hochstelle ↗
Was wäre kein lokales Maximum?
- Betrachte wieder den Graphen von f(x)=x³-3x ↗
- Ganz rechts geht der Graph nach oben weg.
- Der Graph verläuft dort oberhalb des Hochpunktes.
- Dort gibt es aber trotzdem keine Hochpunkte.
Was ist das absolute Maximum?
- Der Überhaupt höchste y-Wert eines Graphen heißt absolutes Maximum.
- Es gibt dann tatsächlich keinen größeren y-Wert mehr.
- Das absolute Maximum im Beispiel wäre plus Unendlich.
Wie bestimmt man ein lokales Maximum?
- Dazu gibt es verschiedene Verfahren.
- Es geht graphisch, rechnerisch, über Probieren oder sonstwie.
- Beschrieben ist das unter Hochpunkte bestimmen ↗