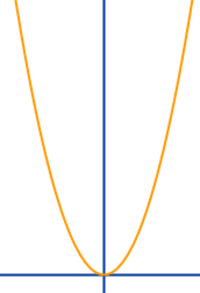
Achsensymmetrie von Graphen überprüfen
Bedeutung | Methoden
Basiswissen
Graphisch und rechnerisch: hier werden Methoden vorgestellt, wie man für eine gegeben Funktionsgleichung überprüft, ob der Graph achsyensymmetrisch zu y-Achse ist.
Was meint Achsensymmetrie?
Wenn von Achsensymmetrie bei einem Graphen die Rede ist, dann ist meistens die Achsensymmetrie zum y-Achse gemeint. Ob ein Graph achsensymmetrisch zur y-Achse ist, kann man mit verschiedenen Methoden überprüfen.
Doppelwegmethode
Man geht auf irgendeinen Punkt auf dem Graphen. Von dort aus geht man auf dem kürzesten Weg zur y-Achse. Dann geht man auf der anderen Seite der y-Achse die gleiche Strecke in gleicher Richtung weiter. Wenn mann dann wieder auf einem Punkt des Graphen herauskommt, und das für alle Punkte des Graphen funktioniert, dann ist der Graph achsensymmetrisch zur y-Achse.
Exponentenmethode
- Funktioniert nur für ganzrationale Funktionen ↗
- Man nimmt dazu nur die Funktionsgleichung.
- Man betrachtet nur die Exponenten von x.
- Exponent ist das Fremdwort für "Hochzahl".
- Sind alle Exponenten von x gerade, ist der Graph achsensymmetrisch zur y-Achse.
- Ein x ohne Hochzahl hat dabei die gedachte "hoch eins": 4x ist wie "4x-hoch-eins".
- Eine Zahl ohne x hat die gedachte Hochzahl 0: 17 ist wie "17-mal-x-hoch-0".
Für die Exponentenmethode betrachtet man alle Exponenten von x. Wichtig ist dass x dasselbe ist wie x hoch 1. Und eine Zahl ist wie Zahl mal x°:
- 4x³ ⭢ der Exponent ist 3 und damit ungerade
- 5x² ⭢ der Exponent ist 2 und damit gerade
- 7x ⭢ ist wie 7x¹ ⭢ der Exponent 1 und damit ist ungerade
- 3 ⭢ ist wie 3x° ⭢ der Exponent ist 0 und damit gerade
Formal
- Man nutzt die Symmetriebedingung:
- f(x) = f(-x)
- Beispiel f(x)=x²
- x² = (-x)² ⭢ x² = x² ⭢ ist achsensymmetrisch
- Beispiel f(x)=x³
- x³ = (-x)³ ⭢ x³ = -x³ ⭢ ist nicht punktsymmetrisch