Fläche unter der Kurve
Integralrechnung
Definition
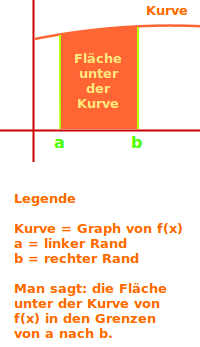
Die Fläche unter der Kurve ist die Flächen zwischen einer Kurve einer Funktion f(x), der x-Achse und - meistens - einer senkrechten Linie als linker Rand und einer senkrechten Linie als rechter Rand. Diese Definition wird hier Schritt-für-Schritt erklärt.
Zusammenfassung
- ∫f(x)·dx ist der rechnerische Ansatz, mehr unter Flächen unter der Kurve berechnen ↗
- Man unterscheidet eine absolute Flächen (Betrag) und eine orientierte Fläche.
Kurve
- Eine Kurve kann eine Parabel, Hyperbel, Gerade oder sonstetwas sein.
- Kurve meint hier den Graph einer beliebigen Funktion.
- Kurve meint hier also Funktionsgraph ↗
Fläche
- Unter der Kurve meint immer:
- Die Fläche zwischen der Kurve und der x-Achse.
- Das gilt auch, wenn die x-Achse oberhalb der Kurve verläuft.
- Dann liegt die Fläche tatsächlich über der Kurve.
- Man spricht aber trotzdem von der Fläche unter der Kurve.
Integrations-Grenzen
- Bei einer Fläche unter der Kurve gibt man immer Grenzen an.
- Es gibt eine linke Grenze, oft mit a abgekürzt.
- Es gibt eine recht Grenze, oft mit b abgekürzt.
- Diese Grenzen heißen auch Integrationsgrenzen.
- a ist der x-Wert bei dem die Fläche anfängt.
- b ist der x-Wert bei dem die Fläche aufhört.
- Die Reihenfolge ist wichtig: a ist links.
Flächengröße
- In der Integralrechnung wird oft die Größe solcher Flächen ausgerechnet.
- Die Größe der Fläche wird berechnet über ein bestimmtes Integral ↗
- Man bildet die Stammfunktion, setzt erst die rechte Grenze b ein ...
- und notiert die Zahl, die dabei herauskommt. Dann setzt man die ...
- linke Grenze a in die Stammfunktion ein und zieht das ab von ...
- der zuvor notierten Zahl. Das Ergebnis ist das bestimmte Integral.
- Der Wert des bestimmten Integral entspricht der Flächenbilanz.
- Die Einheit der Fläche wird oft mit FE angegeben (Flächeneinheiten)
Flächenbilanz
- Flächen unter der x-Achse haben ein negatives Vorzeichen.
- Flächen über der x-Achse haben ein positives Vorzeichen.
- Das kommt automatisch auch beim bestimmten Integral heraus.
- Verläuft eine Kurve teilweise unter und teilweise über der x-Achse, ...
- dann "verrechnet" das bestimmte Integral negative und positive Flächen miteinander.
- Liegt die Kurve halb unter und halb über der x-Achse, ist die Flächenbilanz = 0.
- Mehr dazu unter Flächenbilanz ↗
Flächenbetrag
- Möchte man erreichen, dass alle Flächen positiv gerechnet werden, ...
- dann verwendet man den soganannten Flächenbetrag.
- Man integriert dazu von Nullstelle zu Nullstelle.
- Mehr dazu unter Flächenbetrag ↗