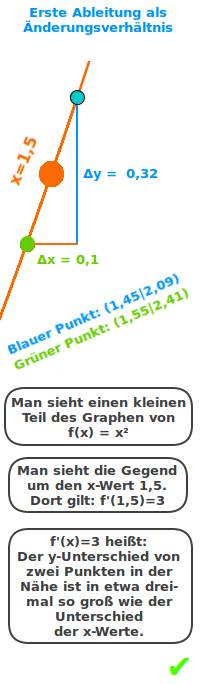
Erste Ableitung als Änderungsverhältnis
f'(x) anschaulich
Basiswissen
Den Wert einer ersten Ableitung kann man graphisch und im Sachkontext auf verschiedene Weisen deuten. Eine Deutung ist: wie viel mal so stark ändert sich y wie x. Dazu werden hier auch praktische Versuche vorgestellt.
Schritt-für-Schritt Erklärung
- Setzt man in f'(x) für x eine konkrete Zahl ein, ...
- dann erhält man auch für f'(x) eine konkrete Zahl.
- Beispiel: Man f'(x) = 2x. Man setzt für x die 3 ein.
- Das ergibt dann für f'(x) die Zahl 6.
- Was bedeutet diese Zahl 6 an der Stelle x=3?
- Das meint: Verändert man in der Nähe von x=3 ...
- den x-Wert geringfügig, dann ändert sich der ...
- dazugehörige y-Wert - oder f(x) ungefähr 6mal so stark.
Quadratflächenwachstum
- x steht für die Seitenlänge eines Quadrates.
- f(x) steht dann für den Flächeninhalt.
- Die Funktionsgleichung ist: f(x)=x²
- Was bedeutet dann f'(x), z. B. bei x=3?
- f'(3) wäre 6. Bei x=3 hat die erste Ableitung den Wert 6.
- Das meint: wenn man in der Nähe von x=3 den x-Wert wenig ändert ...
- dann ändert sich der y-Wert - also f(x) - ungefähr 6 mal so viel.
- Dazu einen Zahlenprobe: Bei genau x=3 ist f(x) genau 9.
- Jetzt erhöhen wir x um 0,1.
- Dann sollte sich der y-Wert um etwa das 6-fache, also um 0,6 erhöhen.
- f(3,1) gibt genau 9,61, das ist ungefähr 0,6 mehr als vorher.
- Es passt also: die erste Ableitung sagt, wie viel mal so viel ...
- sich der y-Wert ändert, wie der x-Wert.
- Siehe auch Kiste 1 Quadratflächenwachstum ↗
Einseitiger Hebel
- Lies die Beschreibung für ein anschauliches Bild.
- Die Funktionsgleichung ist f(x) = 10:x
- Die erste Ableitung ist: f'(x) = -10:x²
- Hält man den Hebel bei x = 2 cm, braucht man 5 Newton Kraft.
- f'(2) ist genau -2,5. Das heißt Folgendes:
- Man man x um 0,1 cm größer, dann müsste die Kraft um das 2,5fache davon abnehmen.
- Die Kraft müsste sich also um 0,25 Newton auf 4,75 Newton verringern.
- Siehe auch WH54 einseitiger Hebel ↗
Kreisumfangswachstum
- Die Funktion "f(x) = Pi mal Durchmesser" beschreibt den Umfang eines Kreises.
- Die erste Ableitung davon ist: f'(x) = pi
- Das sagt: wenn man den Durchmesser eines beliebigen Kreises ...
- um einen kleinen Betrag delta-x verändert, dann verändert sich ...
- der Umfang dort um etwa das 3,14fache.
- Siehe auch Kiste 1 Kreisumfangswachstum [Versuch] ↗
Gummibandversuch
- Hintergrund ist quintische Funktion aus Gummibandversuch ↗
- Eine ganzrationale Funktion vom Grad 5 beschreibt die Längung eines Gummibandes.
- Das Funktionsargument x steht für das unten angehängte Gewicht in Gramm.
- Der Funktionswert f(x) steht für die Gesamtlänge des Gummibandes.
- Eine beliebige Stelle x meint dann anschaulich eine bestimmte Länge.
- Die Ableitung an einer beliebigen Stelle sagt dann, wie viel mal ...
- so stark sich der f(x)-Wert ändern würde wie der x-Wert, wennn ...
- man bei dieser Länge noch etwas Zusatzgewicht unten anhängt.
- Mehr unter quintische Funktion aus Gummibandversuch ↗
Pythagoreischer Aufzug
- An eine Wand ist eine Art Seilaufzug installiert.
- Zieht man an einem Seil, hebt sich an anderer Stelle ein Gewicht.
- Lies mehr dazu unter pythagoreischer Aufzug ↗