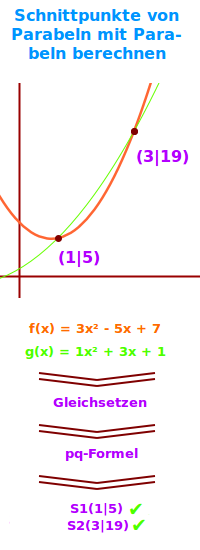Schnittpunkte von Parabeln mit Parabeln berechnen
Schritt-für-Schritt Anleitung
Basiswissen
Parabel meint hier den Graph einer quadratischen Funktion. Ein Schnittpunkt ist jeder Punkt, der gleichzeitig auf zwei Parabeln liegt. Dazu gibt es ein Berechnungsmethode, die immer funktioniert.
Lösungsidee
- Schnittpunkte sind Punkte, die gleichzeitig auf zwei Parabeln liegen.
- Im Schnittpunkt sind also die x- und y-Werte von beiden Parabeln gleich.
- Dies drückt man mathematisch durch Gleichsetzen der Gleichungen aus.
1. Umstellen
- 1. Man hat zwei Parabelgleichungen gegeben.
- 1. Beide müssen auf der linken Seite das y alleine stehen haben.
- 1. Statt y steht oft links auch ein f(x). Beides meint hier dasselbe.
- 1. Falls ein y noch nicht links alleine steht, muss man erst umstellen.
- 1. Parabel a gegeben: -7 = 3x² - 5x - y
- 1. Parabel b gegeben: y = 1x² + 3x + 1
- 1. Parabel a umgestellt: y = 3x² - 5x + 7
- 1. Parabel b umgestellt: y = 1x² + 3x + 1
2. Gleichsetzen
- 2. Auf beiden Seiten steht jetzt das y alleine.
- 2. Im nächsten Schritt setzt man die rechten Seiten gleich:
- 2. 3x² - 5x + 7 = 1x² + 3x + 1
3. Lösen
- 3. Man hat eine Gleichung mit nur noch einer Unbekannten (x).
- 3. Vom Typ her ist das bei Parabeln immer eine quadratische Gleichung.
- 3. Man bringt diese Gleichung durch Umformungen in die Normalform.
- 3. Die Normalform einer quadratischen Gleichung ist: 0 = x² + px + q
- 3. 3x² - 5x + 7 = 1x² + 3x + 1 | -1x² | -3x | -1
- 3. 2x² - 8x + 6 = 0 | :2
- 3. x² - 4x + 3 = 0 | Seiten tauschen
- 3. 0 = x² - 4x + 3 = 0
- 3. Jetzt die pq-Formel benutzen (geht immer):
- 3. Die Lösungen sind dann:
- 3. x = 1
- 3. x = 3