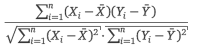Korrelationskoeffizient nach Pearson berechnen
Anleitung
Basiswissen
Ein Zusammenhangs- bzw. Assoziationsmaß gibt in der multivariaten Statistik die Stärke und bei bestimmten Arten auch die Richtung eines Zusammenhangs zweier statistischer Variablen wieder. Der Korrelationskoeffizient nach Pearson ist ein Beispiel dafür. Er kann auf verschiedene Weisen berechnet werden. Hier stehen zwei Varianten kurz erklärt.
Gegeben
- Es sind drei Wertepaare gegeben:
- (1|1) (2|3) (3|5)
1. Schritt
Bilde den Durchschnitt aller x-Werte, hier: 2
2. Schritt
Bilde den Durchschnitt aller y-Werte, hier: 3
3. Schritt
Rechne für alle Wertepaare:
(x-Wert minus x-Durchschnitt) mal (y-Wert minus y-Durchschnitt)
Und addiere alle diese Produkte zusammen, das gibt hier: 4
Diese Zahl schreibst du in den Zähler eines gedachten Bruches.
Der Nenner wird im nächsten Schritt berechnet.
4. Schritt
Rechne für alle Wertepaare:
(x-Wert - minus x-Durchschnitt) hoch zwei
Rechne alle diese Quadrate zusammen und ziehe daraus die Wurzel, ist hier: Wurzel 2
5. Schritt
Rechne für alle Wertepaare:
(y-Wert - minus y-Durchschnitt) hoch zwei
Rechne alle diese Quadrate zusammen und ziehe daraus die Wurzel, ist hier: Wurzel 8
6. Schritt
Multipliziere die Wurzeln aus Schritt 4 und 5.
Nutze das Gesetz: (Wurzel a) mal (Wurzel b) = Wurzel (a mal b)
Hier wird das Ergebnis: glatt 4
Das ist der Nenner des in Schritt 3 angefangenen Bruches.
7. Schritt
Rechne den Wert des Bruches aus Zähler und Nenner aus, das gibt hier: 1
Das ist der Korrelationskoeffizient nach Pearson.
In dem Beispiel hier korrelieren die x und y-Werte perfekt. In einem Graphen würde das heißen, dass die Wertepaare als Punkte im Koordinatensystem eine perfekte Geraden gäben. Das tun sie auch.
Undefiniert
Es gibt den Fall, dass der Nenner in der Formel zu Null wird. Das wäre eine Division durch Null. Eine Division durch Null weist in der Mathematik auf undefinierte Fälle in. Das ist auch hier so: Wird der Nenner zu Null, gibt es keinen Korrelationskoeffizienten. Dieser Fall tritt immer auf, wenn die Punkte in einem Koordinatensystem parallel zur x-Achse verlaufen. Das ist hier in unserem Beispiel nicht der Fall.
Fehlt 1/n?
Die Formel für diesen Korrelationskoeffizienten findet man in verschiedenen Formen. Es gibt auch die Formel, bei der im Zähler ein 1/n oder ein 1/(n-1) steht. n ist die Anzahl der x-y-Wertepärchen. Dann findet man aber auch im Nenner unter jeder der beiden Wurzeln diesen Term. Insgesamt kürzen sich die drei Terme aber wieder weg. In der Beschreibung hier wurde die Variante nach dem kürzen gewählt. Beide Formeln geben aber immer das gleiche Ergebnis.
Zähler = Kovarianz?
Ja und nein: Verwendet man die Formel mit dem 1/n im Zähler, dann ist der Zähler auch identisch mit der Kovarianz. Bei der hier oben verwendeten Formel fehlt aber das 1/n. Hier ist also der Zähler nicht identisch mit der Kovarianz.
Welche alternative Formel gibt es?
r = Kovarianz geteilt durch [(Standardabweichung der x-Werte) mal (Standardabweichung der y-Werte)]
Was sagt dieser Korrelationskoeffizient aus?
Der Korrelationskoeffizient nach Pearson gibt an, wie gut zwei Größen sich mit je-desto Sätzen in ihrer Veränderung beschreiben lassen: je mehr CO2 in der Atmosphäre, desto höher ist die globale Temperatur: wie gut dieser Satz gilt, kann für bestimmte Datensätze als Zahlenwert von -1 bis 1 angegeben werden. Mehr zur Bedeutung steht im Artikel Korrelationskoeffizient nach Pearson ↗