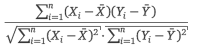Korrelationskoeffizient nach Pearson berechnen
10 Textaufgaben für Obertufe/Studium
Die Zahlen für die Aufgaben a bis e sind so gewählt, dass man den Korrelationskoeffizienten ohne Taschenrechner berechnen kann. Durch das Rechnen von Hand kriegt man ein gutes Gefühl für das Rechenschema.
Skizziere die Punkte grob von Hand in einem Koordinatensystem.
Berechne den Korrelationskoeffizienten nach Pearson.
Es kommen nur raus: -1; 0; 1 und "nicht definiert":
a) (10|20) (20|30) (30|40) (40|50)
b) (10|50) (20|40) (30|30) (40|20)
c) (10|40) (20|30) (30|30) (40|40)
d) (10|2) (10|0) (10|0) (10|2)
e) (1|-1) (2|-2) (3|-3) (4|-4)
Bei den folgenden Aufgaben sind die Ergebnisse normalerweise alle Dezimalzahlen. Rechne mit dem Taschenrechner und runde das Ergebnis auf eine Nachkommastelle. Formuliereimmer auch einen Satz zur Interpretation. Benutze Formulierungen wie "Der Korrelationsfaktor liegt fast bei 1, also gibt es einen engen positiven Zusammenhang zwischen...".
f) Flüsse
Wie viel Wasser in einer bestimmten Zeit an einer bestimmten Stelle eines Flusses vorbeifließt nennt man in der Geographie den Durchfluss. Die x-Werte der folgenden Datenpaare stehen für die Länge eines Flusses in Kilometern. Die y-Werte stehen für den Durchfluss an der Flussmündung in Kubikmetern pro Sekunde:
Wurm (52|1.4)
Rhein (1239|2900)
Ganges (2620|13000)
Sambesi (2574|7070)
g) Meereis
Als Meereis bezeichnen Klimaforscher das auf dem Ozean schwimmende Eis in den Polargebieten. Im Winter ist es mehr, im Sommer ist es weniger. Satelliten beobachten seit den 1970er-Jahren, wie viele Quadratkilometer Ozean vom Meereis bedeckt sind. Für die Arktis (Nordpol) ist die größte Ausdehnung immer am Ende des Winters im März erreicht. Im Sommerhalbjahr schrumpft die Eisfläche dann wieder bis etwa September. Der x Wert der Daten unten wäre die Jahreszahl, der y-Wert wäre die Ausdehnung des arktischen Meereises in Millionen Quadratkilometern jeweils im Monat März:
1980 1,578 Mio. qkm
1990 1,575 Mio. qkm
2000 1,506 Mio. qck
2010 1,488 Mio. qkc
h) Atomgewichte
Betrachtet man einzelne Atome, so kann man ihnen eine Masse zuordnen. Manche Atome sind leicht, andere sind schwer. In der Physik und Chemie nimmt man als Vergleich das Gewicht von einem Proton. Das ist abgekürzt die "atomare Masseneinheit", kurz u. Ein Atomgewicht von 27u meint dann, dass das Atom 27 mal so schwer ist wie ein Proton. Etwas anderes bedeutet das Wort Dichte: hierunter versteht man, wie viel Gramm jeder Kubikzentimeter eines reinen (elementaren) Stoffes wiegt. Wenn man sagt, dass Eisen eine Dichte von etwa 8 hat, dann meint das: ein Kubikzentimeter Eisen wiegt rund 8 Gramm. In der Tabelle unten findest du Atomgewichte gerundet auf ganze Zahlene (x-Wert) sowie die Dichte des Elementes gerundet auf eine Nachkommastelle (y-Wert).
Wolfram: Atomgewicht 184 u, Dichte 19,3
Aluminium: Atomgewicht 27 u Dichte 2,7
Schwefel: Atomgewicht 32 u, Dichte 2,1
Eisen: Atomgewicht 56 u, Dichte 7,9
i) Quersummen
Die Quersumme einer Zahl ist die Summe ihrer Ziffernwerte. Beispiel: die Quersumme von 27 ergibt sich aus 2 plus 7, ist also 9. Die Quersumme von 100 hingegen ist nur 1. Wie plausibel ist die Vermutung, dass größere Zahlen tendeziell auch größere Quersummen haben? Untersuche die Korrelation einmal für die Zahlen 91, 92, 93 und 94. Berechne dann die Korrelation für die Zahlen 98, 99, 100 und 101. Vergleiche die Ergebnisse und ziehe einen (vorläufigen) Schluss.
j) Lebenserwartung
Klingt das plausibel: Menschen mit einem hohen Einkommen haben einen stressigeren Beruf. Und wer viel Stress hat, lebt nicht so lange. Oder müsste man eher umgekehrt denken: wer viel verdient ist zufriedener, weniger Stress und damit eine höhere Lebenserwartung? Die Daten unten sprechen eine klare Sprache. Links (x-Wert) steht das monatliche Bruttoeinkommen in Euro, in der Mitte die Lebenserwartung für Frauen in Jahren, ganz rechts die Lebenserwartung von Männern in Jahren:
wen. als 1500 Euro || Frauen 78,4 Jahre || Männer 71,1 Jahre
1500 bis 2500 Euro || Frauen 83,5 Jahre || Männer 75,5 Jahre
2500 bis 3500 Euro || Frauen 85,0 Jahre || Männer 75,6 Jahre
3500 bis 4500 Euro || Frauen 86,0 Jahre || Männer 77,8 Jahre
mehr als 4500 Euro || Frauen 86,2 Jahre || Männer 80,0 Jahre
Berechne den Korrelationskoeffizienten nach Pearson entweder für Frauen oder für Männer (in der Lösung stehen beide Ergebnisse). Nimm als x-Wert 1000 Euro für Geringstverdiener, 5000 Euro für die Topverdiener und ansonsten den Mittelwert der Klassen.
Quelle: K. W. Lauterbach (Mitglied des Bundestages und andere: "Ein Zusammenhang zwischen Einkommen und Lebenserwartung". Die Daten basieren auf Befragungen und Erhebungen aus den Jahren 2000 bis 2004.