Gegenkathete über Sinus
Wie man die Länge einer Gegenkathete mit dem Sinus ausrechnet
Basiswissen
Die Länge der Kathete gegenüber vom gegebenen Winkel: es gibt verschiedene Methoden, diese Länge zur berechnen
Vorab
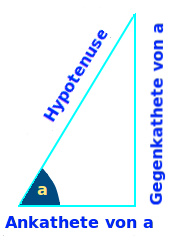
- Die Hypotenuse ist die längste Seite in einem rechtwinkligen Dreieck.
- Die Hypotenuse liegt immer gegenüber vom rechten Winkel.
- Die zwei Seiten direkt am 90-Grad Winkel heißen Katheten.
- Die Katheten sind immer die zwei kürzen Seiten im Dreieck.
- Neben dem 90-Grad-Winkel gibt es noch zwei spitze Winkel.
- Spitz meint hier: weniger als 90 Grad.
- Einer dieser Winkel muss bekannt sein.
- Wir nennen ihn hier alpha.
- Auch die Länge der Hypotenuse muss bekannt sein.
- Die Kathete gegenüber von Alpha heißt Gegenkathete.
- Gesucht ist die Länge GK der Kathete gegenüber von alpha.
Formeln
- sin(a) = Gegenkathete durch Hypotenuse
- Gegenkathete = Hypotenuse mal sin(a)
Berechnung
- Nimm die Länge der Hypotenuse. Wir nennen sie HY.
- Bestimme den Sinus von alpha.
- Rechne HY mal dem Sinus von alpha.
- Das Ergebnis ist die Länge der Gegenkathete GK.
Zahlenbeispiel
- Dreieck hat einen Winkel von 45 Grad an der Hypotenuse.
- Die Hypotenuse ist 8 cm lang.
- Der Sinus von 45 Grad ist etwa 0,7.
- 8 cm mal 0,7 gibt 5,6 cm.
- Die Gegenkathete ist ungefähr 5,6 cm lang.