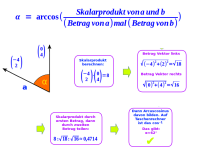
Winkel über Skalarprodukt
Anleitung
Basiswissen
Man hat zwei Vektoren gegeben und sucht den Winkel, den sie miteinander bilden: man teilt das Skalarprodukt der beiden Vektoren durch das Produkt ihrer jeweiligen Beträge. Davon nimmt man dann den Arcuscosinus (cos hoch -1). Das Ergebnis ist der gesucht Winkel. Das ist hier mit einem Zahlenbeispiel Schritt-für-Schritt erklärt.
Beispiel-Rechnung
- Man hat zwei Vektoren gegeben.
- Beispiel: Vektor A=(3|4|0) und Vektor B(5|12|0)
- Zur Definition siehe auch Winkel zwischen Vektoren ↗
Formel
- alpha = arccos [(a·b)/(|a|·|b|)]
Legende
- alpha = der gesuchte Winkel
- a·b = Skalarprodukt von a und b
- |a| = der Betrag (Länge) des Vektors a
- |b| = der Betrag (Länge) des Vektors b
Erläuterung
- Man schreibt einen großen Bruchstrich.
- Man berechnet dann a·b, das ist das Skalarprodukt ↗
- Das gibt im Beispiel: 63
- Das Ergebnis wird als Zahlenwert oben auf den Bruchstrich geschrieben (Zähler).
- Man berechnet dann für die beiden Vektoren getrennt den Vektorbetrag ↗
- Für A ist der Vektorbetrag genau 5, für B ist der Vektorbetrag genau 13.
- Die beiden Beträge schreibt man beide in den Nenner des Bruches.
- Sie werden dort multipliziert, also mit einem Malpunkt verbunden.
- Der gesamte Bruch hat im Beispiel jetzt die Form: 63/(5·13)
- Den Wert des Bruches berechnen, gibt etwa: 0,97
- Von diesen Wert den Arcuscosinus berechnen (Taschenrechner).
- Auf einem Taschenrechner ist das oft Cosinus hoch minus eins ↗
- Das Ergebnis ist der kleinere Winkel zwischen den Vektoren
- Im Beispiel ist alpha etwa 14°.
Beispiele
- Die Vektoren (10|0|0) und (0|4|0) bilden einen Winkel von genau: 90°
- Die Vektoren (10|1|1) und (2|9|1) bilden einen Winkel von etwa: 71°
- Die Vektoren (10|1|1) und (9|1|1) bilden einen Winkel von etwa: 1°