Uneigentliches Integral

∫f(x)·dx von a bis z über Limes

Basiswissen

Was meint Integral?

• Das uneigentliche Integral ist ein bestimmtes Integral ↗
  

• Bestimmt meint: der linke und rechte Rand sind angegeben (bestimmt).
  

• Ein Integral ist ein Zahlenwert, der die Größe einer Fläche angeben soll.
  

• Fläche meint hier die Fläche zwischen einem Funktionsgraphen und der x-Achse.
  

Was meint uneigentliches Integral?

• Es gibt Flächen, die gedanklich keine feste Grenze haben.
  

• Der Graph kann zum Beispiel nach oben oder rechts offen sein.
  

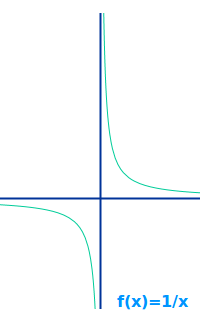
• Ein häufig gewähltes Beispiel ist die Normalhyperbel f(x)=1:x ↗
  

• Angenommen man sucht die Fläche von x=1 bis x=unendlich.
  

• Die untere Flächenrand ist die x-Achse. Das ist OK.
  

• Der linke Flächenrand ist ein senkrechter Strich, auch OK.
  

• Der obere Flächenrand ist der Funktionsgraph, auch OK.
  

• Der rechte Flächenrand ist aber offen.
  

• Der rechte Rand ist angegeben, aber nicht fest.
  

• Das meint uneigentliches Integral:
  

• Ein Flächenrand ist nicht fest abgeschlossen.
  

• Trotz eines offenen Randes kann oft ein eindeutiger Flächenwert berechnet werden.
  

• Aber nicht immer: manchmal wächst die Fläche ins Unendliche.
  

• Was zutrifft, ergibt sich während der Flächenberechnung.
  

Welche Arten werden unterschieden?

• Die offene Grenze kann auf zwei Weisen entstehen.
  

• Man kann auf der x-Achse bis unendlich gehen wollen.
  

• (Bis minus unendlich fällt mit unter diesen Fall.)
  

• Diese Variante heißt uneigentliches Integral erster Art ↗
  

• Oder der Funktionswert geht an einer Stelle ...
  

• Richtung plus oder minus unendlich
  

• Das wäre ein uneigentliches Integral zweiter Art ↗
  

Wie löst man entsprechende Aufgaben?

• Nicht alle uneigentlichen Integrale sind lösbar.
  

• Um es zu probieren gibt es verschiedene Methoden.