Steigung aus Steigungsdreieck
Berechnung
Basiswissen
Man hat ein fertiges Steigungsdreieck und will daraus die Steigung bestimmen: man rechnet einfach: die Höhe des Steigungsdreiecks geteilt durch die Breite des Steigungsdreiecks. Das Ergebnis ist die Steigung vom linken zum rechten Punkt auf dem Graphen. Das ist hier näher erklärt.
Vorab
- Hier wird erklärt, wie man die Steigung abliest, wenn man schon ein Steigungsdreieck hat.
- Wie man ein Steigungsdreieck zeichnet steht unter Steigungsdreieck aus Graph ↗
- Die Steigung wird oft mit einem kleinen m abgekürzt.
- Die Regel gilt für Geraden aber auch andere Graphen.
- Siehe auch Steigungsdreieck ↗
Steigung ablesen
- Das Steigungsdreieck hat eine senkrechte Seite (parallel zur y-Achse).
- das Steigungsdreieck hat eine waagrechte Seite (parallel zur x-Achse).
- Die Steigung m ist: Länge der senkrechten Seite geteilt durch Länge der waagrechten Seite.
- Für diese Methode müssen aber die x- und y-Achse gleich skaliert sein.
- Das heißt: jeder Zentimeter auf der x-Achse muss genauso viel meinen ...
- wie ein Zentimeter auf der y-Achse. Ansonsten erhält man falsche Werte.
- Gilt das nicht, wählt man besser eine andere Methode.
- Siehe dann z. B. unter Geradensteigung aus zwei Punkten ↗
Beispiele
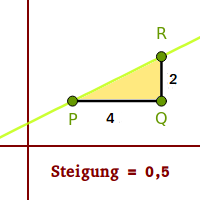
- Wenn die senkrechte Seite 2 lang ist ...
- und die waagrechte Seite 4 lang ist, ...
- dann ist die Steigung m=2/4 oder 0,5.
Steigung berechnen
- Wenn man das Steigungsdreick hat, kann man auch die Steigungsformel benutzen.
- Dazu markiert man die zwei Eckpunkte des Dreiecks, die auf dem Graphen liegen.
- Den y-Wert des rechten Punktes nennt man Y2.
- Den y-Wert des linkes Punktes nennt man Y1.
- Den x-Wert des rechten Punktes nennt man X2.
- Den x-Wert des linken Punktes nennt man X1.
- Die Steigung m ist dann: (Y2-Y1)/(X2-X1)
- Der Term ist der Differenzenquotient ↗
Tipps
- Das Steigungsdreieck bei Geraden möglichst groß machen.
- Bei allen anderen Funktion: Steigungsdreieck möglichst klein machen.