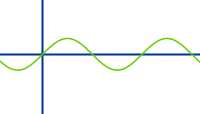
Sinusfunktion
Basiswissen
f(x)=sin(x): gibt für jeden Winkel den dazugehörigen Sinuswert an. Der Sinus wird zunächst nur rechtwinklige Dreiecke definiert und gilt nur für Winkel zwischen 0° bis 90°. In einer Verallgemeinerung wird der dann für beliebige große und auch negative Winkel am sogenannten Einheitskreis definiert. Das macht die Sinusfunktion.
Die elementare Sinusfunktion
Spricht man von DER Sinusfunktion, meint man damit meist die einfachstmögliche, die sogenannte elementare Sinusfunktion. Siehe dazu den Artikel f(x)=sin(x) ↗
Was ist der Unterschied zwischen Sinus und Sinusfunktion?
- Der Sinus an sich ist zunächst nur definiert für Werte kleiner 90° ↗
- Das entspricht der anschaulichen Bedeutung des Sinus in einem Dreieck ↗
- Über eine Definition am Einheitskreis wird der Sinus verallgemeinert.
- Er geht über rechtwinklige Dreiecke hinaus und gilt für beliebige Zahlen.
- Lies mehr unter trigonometrische Funktion ↗
Definitions- und Wertebereich der Sinusfunktion
- Für die elementare Sinusfunktion f(x)=sin(x) gilt:
- x kann ersetzt werden durch jede beliebige reelle Zahl ↗
- Der Definitionsbereich für x ist die Menge der reellen Zahlen.
- Für y können dann nur Werte zwischen -1 und 1 herauskommen.
- Der Wertebereich ist dann das Intervall [-1|1] ↗
- Siehe auch unter Definitionsbereich ↗
- Oder Wertebereich ↗
Transformationen für Sachthemen
- Die Sinusfunktion spielt für viele Sachthemen eine wichtige Rolle.
- Sie beschreibt oft periodische Vorgängen (Tag/Nach, Jahreszeiten, Schwingungen).
- Zur Anpassung an den gegebenen Sachverhalt wird der Graph oft transformiert.
- Oft wird er gestreckt oder gestaucht, auch entlang der x-Achse.
- Man spricht dann allemeiner von Sinusfunktionen ↗