Senkrechte Geraden
Mathematik
Einordnung
Eine Gerade heißt senrecht, wenn sie mit einem Winkel von 90° auf die Erdoberfläche triffe. Zwei Geraden sind zueinander senkrecht, wenn sie sich mit einem Winkel von 90° schneiden.
Was heißt Gerade in diesem Artikel?
- Eine Gerade ist eine unendlich lang gedachte Strecke.
- In der Mathematik betrachtet man Geraden in 2D und in 3D-Koordinatensystemen.
- Zu Geraden in 3D-Koordinatensystemen (xyz), siehe unter orthogonale Geraden ↗
- In diesem Artikel geht es um Geraden in einem 2D-Koordinatensystem [xy] ↗
Geraden senkrecht zur Erdoberfläche
Eine Linie, die direkt nach oben in den Himmel und/oder direkt nach unten Richtung Boden zeigt nennt man senkrecht oder auch lotrecht. Ein gerader Baum steht normalerweise senkrecht zum Boden. Ein Stein fällt normalerweise entlang einer senkrecht gedachten Geraden zum Boden (freier Fall). Lies mehr unter senkrecht ↗
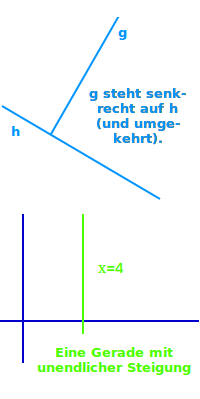
Geraden mit unendlicher Steigung
Definiert man in einem xy-Koordinatensystem eine Gerade über die Gleichung x=4, so ist steht dazugehörige Graph senrecht auf der x-Achse des Koordinatensystem. Er verläuft entsprechend parallel zur y-Achse. Die Steigung dieser Geraden ist nicht definiert oder unendlich. x=4 steht nicht für eine Funktion sondern für eine Zuordnung oder eine sogenannte Ortlinie. Mehr unter Gerade mit unendlicher Steigung ↗
Geraden senkrecht zu anderen Geraden (2D)
Definiert man in einem xy-Koordinatensystem zwei Geraden, dann stehen sie genau dann senkrecht aufeinander, wenn an ihrem Schnittpunkt ein 90°-Winkel auftritt. Für solche Geraden gilt immer, dass das Produkt ihrer Steigungen genau die Zahl -1 ergibt. Kennt man die Steigung von einer der zwei Geraden, bildet man von ihr den Kehrwert und davon die Gegenzahl. Das gibt die Steigung der anderen Geraden. Lies mehr unter zueinander senkrechte Geraden ↗