Schnittpunkte von Parabeln mit Geraden berechnen
Ein Schema, das immer geht
Basiswissen
◦ Die Gleichung einer Geraden ist eine lineare Funktion.
◦ Die Gleichung einer Parabel ist eine quadratische Funktion.
◦ Beispiel Gerade: f(x) = 4x + 2
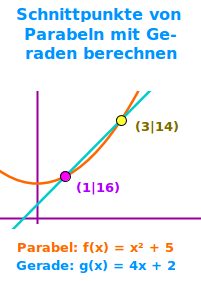
◦ Beispiel Parabel: f(x) = xx + 5
◦ Man setzt die rechten Seiten dann immer gleich:
◦ Gleichsetzen: 4x + 2 = xx + 5
◦ Die Gleichung dann in die Normalform umformen:
◦ 0 = xx - 4x + 3
◦ Die Gleichung dann mit der pq-Formel lösen:
◦ x1=3 und x1=1
◦ Das sind die x-Werte der Schnittpunkte.
◦ Jetzt noch die y-Werte der Schnittpunkte berechnen:
◦ x1 und x2 dann in Geradengleichung einsetzen:
◦ x1 gibt y1=14 und x2 gibt 6
◦ Ergebnis explizit (ausdrücklich) hinschreiben:
◦ S1(3|14) und S2(1|6)
Besonderheiten
◦ Liefert die pq-Formel nur eine Lösung, gibt es nur einen Schnittpunkt.
◦ Liefert die pq-Formel keine Lösung, gibt es keine Schnittpunkte.
Siehe auch
=> Schnittpunkte von Parabeln mit Geraden
=> qck
