Satz des Pythagoras
a² + b² = c²
Basiswissen
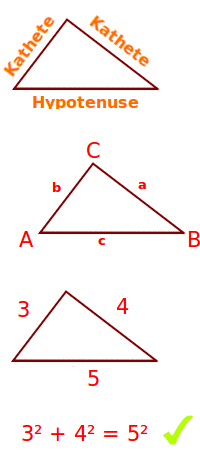
Man hat ein rechtwinkliges Dreieck mit drei Seiten: a, b und c. c ist dabei die längste Seite. Man misst die Länge jeder der drei Seiten. Dann multipliziert man die Länge jeder Seite mit sich selbst. Man erhält drei Zwischenergebnisse: a², b² und c². Dann addiert man a² und b². Die daraus entstehende Summe ist immer gleich (oder sehr nahe bei) c². Kurz: a²+b² = c²
Einführung zum Satz des Pythagoras
Der Satz des Pythagoras gilt nur für rechtwinklige Dreicke (genau ein 90°-Winkel) und alle rechtwinkligen Dreiecke. Er besagt: multipliziert man die Längen der beiden kürzeren Seiten (Katheten) mit sich selbst und addiert diese Zwischenergebnisse zusammen, erhält man immer dasselbe Ergebnis wie bei der Multiplikation der längsten Seite (Hypotenuse) mit sich selbst. Mit Hilfe dieser Formel genügt es, bei einem rechtwinkligen Dreieck die Länge von zwei Seiten zu kennen. Man kann dann die Länge der dritten Seite immer berechnen.
Formel für den Satz des Pythagoras
- a² + b² = c²
Legende
- a = Länge von einer Kathete ↗
- b = Länge der anderen Kathete ↗
- c = Länge der Hypotenuse ↗
Was sind die Katheten (a und b) und was die Hypotenuse (c)?
- a² meint dasselbe wie a mal a.
- Der Satz des Pythagoras gilt nur für ein rechtwinkliges Dreieck ↗
- Der Satz des Pythagoras gilt für alle rechtwinkligen Dreiecke.
- In einem rechtwinkligen Dreieck gibt es immer eine Hypotenuse ↗
- Die Hypotenuse liegt immer gegenüber vom rechten Winkel ↗
- Die Hypotenuse ist immer die längste Seite im Dreieck.
- Das c in der Formel steht immer für die Länge der Hypotenuse.
- Die beiden anderen Seiten heißen Katheten ↗
- Die Katheten sind die Schenkel des rechten Winkels.
- Die Katheten sind immer die zwei kürzeren Seiten.
- Das a ist die Länge von einer der beiden Katheten.
- Das b ist die Länge der anderen der beiden Katheten.
Der Satz des Pythagoras rein rechnerisch
- Man nimmt die Länge einer Kathete mit sich selbst mal.
- Mit sich selbst malnehmen nennt auch hoch zwei rechnen oder quadrieren ↗
- Man nimmt die Länge der anderen Kathete mit sich selbst mal.
- Man addiert diese beiden Ergebnisse.
- Wenn man die Länge der Hypotenuse mit sich selbst malnimmt, …
- kommt dabei immer dieselbe Zahl heraus.
Der Satz des Pythagoras geometrisch gedeutet
- Man nimmt eine der zwei Katheten.
- Man nennt diese Seite und ihre Länge a.
- Man betrachtet sie als eine von vier Seiten von einem Quadrat ↗
- Man zeichnet dann damit ein Quadrat, das ist das Quadrat „über der ersten Kathete“.
- Man macht dasselbe dann mit der zweiten Kathete und mit der Hypotenuse.
- Die zweite Kathete und ihre Länge nennt man b, die Hypotenuse nennt man c.
- Man hat dann also insgesamt drei Quadrate gezeichnet.
- Man berechnet dann für jedes Quadrat einzeln die Quadratfläche ↗
- a mal a oder kurz a² gibt den Inhalt des ersten Quadrates.
- b mal b oder kurz b² gibt den Inhalt des zweiten Quadrates.
- c mal c oder kurz c² gibt den Inhalt des dritten Quadrates.
- Dann addiert man die ersten beiden Flächen.
- Diese Summe gibt genau die Fläche des dritten Quadrates.
- Man sagt: die Summe der Quadrate über den zwei Katheten, …
- ist vom Zahlenwert her gleich dem Quadrat über der Hypotenuse.
Was ist der Nutzen dieses Satzes?
- Kennt man von einem rechtwinkligen Dreieck die Längen von zwei ...
- Seiten, dann kann man die Länge der dritten Seite ausrechnen.
- Dazu benötigt man unterschiedliche Rechenwege.
Wie berechnet man die Länge der Hypotenuse?
- Bekannt sind: a und b
- Z. B. a=5 und b=12
- Man geht aus von: a²+b² = c²
- c ist die Länge der gesuchten Hypotenuse.
- Man formt die Gleichung um nach c:
- a²+b² = c² | auf beiden Seiten die Wurzel ziehen
- Wurzel von (a²+b²) = c
- Einsetzen: Wurzel von (5²+12²) = 13
- Die gesuchte Länge von c ist: 13
- Mehr dazu unter Hypotenuse über Pythagoras => pdf ↗
Wie berechnet man die Länge einer der beiden Katheten?
- Man geht aus von: a²+b² = c²
- c ist die Hyptonuse, also die längste Seite.
- a ist eine der zwei Katheten, b die andere.
- Es ist für a und b egal, wer die längere ist.
- Man formt um nach zum Beispiel a:
- a² + b² = c² | -b²
- a² = c²-b² | Wurzel ziehen
- a = Wurzel aus (c²-b²)
- Zahlenbeispiel: c=5 und b=4. Wie lang ist a?
- Einsetzen: a = Wurzel aus (5²-4²)
- a = Wurzel aus (25-16) = 3
- Die gesuchte Kathete hat die Länge 3.
- Mehr dazu unter Kathete über Pythagoras => pdf ↗
Gilt der Satz des Pythagoras immer?
Solange man rechtwinklige Dreiecke auf flachen, ungekrümmten Flächen zeichnet, etwa auf einem glatten Stück Papier auf einem Tisch, dann stimmt der Satz immer. Interessant ist jetzt ein Gedankenexperiment, bei dem der Satz zunehmend nicht mehr stimmt. Man stellt sich die Erde als völlig perfekte Kugel vor. Wir leben dann gedanklich auf dieser Kugeloberlfäche. Nun zeichnen wir ein kleines rechtwinkliges Dreieck. Wenn wir die Seitenlängen messen und damit den Satz des Pythagoras überprüfen wird er (abgesehen von kleinen Messungenauigkeiten) immer sehr gut aufgehen, also stimmen. Machen wir das Dreieck aber gedanklich sehr groß, dann geht die Gleichung immer schlechter auf. Der Grund ist dass war nicht auf einer glatten ebenen Fläche zeichnen, sondern auf einer gekrümmten Kugeloberfläche[1]. Tatsächlich gibt es ein großes Gebiet der Geometrie, das sich mit Figuren auf Kugeloberflächen beschäftigt. Das ist die sogenannte sphärische Geometrie. Ein sehr interessanter Fall zu diesem Gedanken ist das von uns so genannte Galapagos-Dreieck ↗
Aufgaben zum Satz des Pythagoras
- => qck [gemischte Aufgaben]
Fußnoten
- [1] Bei Gesetzen spricht man von einem sogenannten Gültigkeitsbereich. Das ist der Bereich der Wirklichkeit für den ein Gesetz ausreichend gut passt. In der Mathematik entspricht dieser Gedanke dem Definitionsbereich.