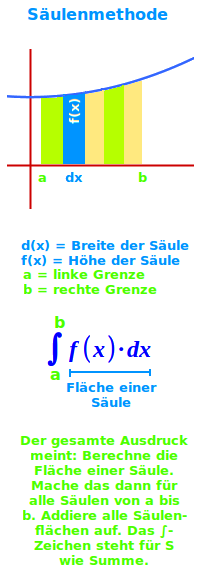
Säulenmethode
Integralrechnung
Basiswissen
∫f(x)·dx mit dem Integral über Ober- und Untersumme: hier wird geometrisch anschaulich erklärt, dass man mit Hilfe der sogenannten Unter- und Obersumme den Flächeninhalt von Flächen mit beliebig geschwungenen Rändern berechnen kann. Der letztendliche Rechenschritt ist das Integrieren. Das wird auf einer anderen Seite erklärt. Das Ergebnis ist eine Zahl und heißt Integral. In diesem Artikel geht es um das geometrische Verständnis des Integrierens.
Definition
Säulenmethode ist kein offizieller mathematischer Fachbegriff. Das Wort wird aber häufig in der Schulmathematik verwendet. Er steht für die Bildung eines Integrals über Ober- und Untersumme.
Begriffe
- ∫f(x)·dx als Ganzes ist ein unbestimmtes Integral ↗
- f(x) ist eine Funktion, als Zahlenwert auch der Funktionswert ↗
- dx ist das Integrationsdifferential ↗
Sinn
- Berechnet werden soll die Fläche zwischen einem Graphen und der x-Achse ↗
- Die Fläche ist oben durch den Graphen, unten durch die x-Achse begrenzt.
- Dabei wird zunächst vorausgesetzt, dass der Graph die Achse nicht schneidet.
- Links und rechts soll die Fläche durch senkrechte Linien begrenzt sein.
- Einfach ist es, wenn die Fläche lückenlos in wenige einfache Flächen zerlegbar ist.
- Solche einfachen Flächen sind z. B. Rechtecke, Dreiecke oder Halbkreise.
- Das ginge zum Beispiel gut bei Geraden, schwer wäre es bei einer Parabel.
- Bei einer Parabel müsste man viele kleine Teilflächen berechnen, was sehr aufwändig wird.
- Ein sehr viel schnelleres Verfahren hin zu einer genauen Fläche ist die Säulenmethode.
- Sie beinhaltet die Bildung einer sogenannten Ober- und einer Untersumme.
Untersumme
- Man zeichnet den Graphen der Funktion.
- Man füllt den Graphen zwischen x-Achse und Kurvenverlauf mit Säulen auf.
- Die Säulen sind alle gleich breit. Sie berühren an einer Ecke immer die Kurve.
- Aber sie werden so gezeichnet, dass die Kurve niemals durch eine Säule verläuft.
- Der Flächeninhalt dieser Säulen zusammengedacht heißt Untersumme.
- Die Untersumme ist immer kleiner als die eigentliche Fläche.
- Dann lässt man gedanklich die Säulen immer schmaler werden.
- Gleichzeitig nimmt dabei die Anzahl der zu zeichnenden Säulen zu.
- Dadurch wird auch die Lücke zwischen Untersumme und echter Fläche immer kleiner.
- Gedanklich lässt man die Anzahl der Säulen dann gegen unenndlich laufen.
- Die fehlende Lücke zur gesuchten Fläche geht dadurch gegen Null.
- Mathematik geschieht das über eine Grenzwertbildung über Summensätze.
- Für diesen Schritt gibt es später einen einfachen Rechenschritt, das Integrieren.
- Tatsächlich erreicht die Untersumme aber niemals den exakten Wert der gesuchten Fläche.
- Um trotzdem zur exakten Fläche zu gelangen, benutzt man zusätzlich noch die Obersumme.
- Siehe auch Untersumme ↗
Obersumme
- Sie gleicht in jeder Hinsicht der Untersumme, mit einer Ausnahme:
- Man zeichnet die Säulen so, dass eine Ecke wieder genau auf der Kurve liegt.
- Man zeichnte sie aber auch so, dass die Kurve immer durch die Säule hindurchgeht.
- Die Summe dieser Säulen ist damit immer größer als die exakte gesucht Fläche.
- Bei der Grenzwertbildung ist ihre Zahl also immer ein klein Bißchen zu groß.
- Wie man trotzdem zum exakten Wert kommt, wird im nächsten Abschnitt erklärt.
- Siehe auch Obersumme ↗
Exakte Fläche
- Es gibt nur genau eine Zahl, die weder von der Unter- noch von der Obersumme ...
- bei der Grenzwertbildung erreicht wird. Sie ist immer größer als die Untersumme ...
- und sie ist immer kleiner als die Obersumme. Es gibt nur genau eine solche Zahl.
- Diese einzig mögliche Zahl ist der exakte Wert des Flächeninhaltes.
- Ihn wie beschrieben zu bestimmen heißt umgangssprachlich Säulenmethode.
- Den Rechenvorgang dazu nennt man Integrieren ↗
Riemann
In der Höheren Mathematik wird die Vorstellung eines Integrals als Summe von unendlich vielen senkrecht stehenden Säulenflächen benannt als Riemannsches Integral ↗
Das Integral als Produktsumme
Das Ergebnis der Säulenmethode nennt man als Zahl auch das Integral. Integrieren hieß früher so viel wie Plusrechnen, was man heute addieren nennt. Tatsächlich addiert man viele Produkte auf, nämlich die Flächen der einzelnen Säulen, die man einzeln berechnet nach Höhe mal Breite. Siehe auch Produktsumme ↗