Reelle Zahl
ℝ: Jede Zahl
Basiswissen
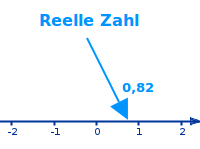
Jede Zahl, die man irgendwo auf einer Zahlengeraden platzieren kann heißt reell. Dazu gehören als natürlichen, negativen, ganzen, gebrochenen oder auch dezimalen Zahlen dazu. Im Prinzip alle Zahlen, die man in der Mittelstufe kennenlernt.
Definition
- Jede Zahl, die man auf der Zahlengeraden eintragen kann heißt reell.
- Das sind zum Beispiel die 3, die -5, die -3,8 oder auch die irrationale Zahl Pi.
- Im Prinzip sind es alle Zahlen, die man bis zur Klasse 10 kennen lernt.
- Beispiele unter reelle Zahlen ↗
Schreibweise
- Häufige kürzt man eine reelle Zahl ab mit r oder x.
- x ∈ ℝ meint: x darf jede reelle Zahl sein.
- Das ℝ meint: alle reellen Zahlen zusammengedacht.
- Sprich: Die Menge der reellen Zahlen
Nicht reell
- In der höheren Mathematik gibt es die soganannten komplexen Zahlen.
- Sie können auch über oder unter der Zahlengeraden liegen.
- Mehr dazu unter keine reellen Zahlen ↗
Beziehungen
- Alle natürlichen Zahlen sind immer auch reell.
- Alle ganzen Zahlen sind immer auch reell.
- Alle rationalen Zahlen sind immer auch reell.
- Alle irrationalen Zahlen immer auch reell.
Aber ...
- Nicht alle reellen Zahlen sind auch natürlich, z. B. die -3.
- Nicht alle reellen Zahlen sind auch ganz, z. B. die -5,3.
- Nicht alle reellen Zahlen sind auch rational, z. B. die Zahl pi.
- Nicht alle reellen Zahlen sind auch irrational, z. B. die 4.
Abkürzung
- Die Menge aller reellen Zahlen wird mit einem großen R abgekürzt.
- Der senkrechte Strich des Großbuchstaben wird dabei gedoppelt geschrieben.