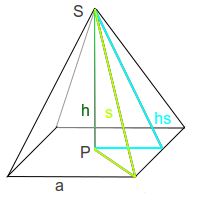
Pyramidenhöhe über Pythagoras
Zwei verschiedene Rechenwege
Basiswissen
In der Mathematik, Physik oder Chemie: kurze Erklärung von Fachworten, Symbolen und Formeln
Vorab
◦ Es gibt zwei verschiedene Methoden.
◦ Die Wahl hängt davon ab, was gegeben ist.
◦ Danach ist die Liste sortiert.
I Halbe Bodendiagonale & Seitenkante s
◦ Man hat ein rechtwinkliges Dreieck.
◦ Die Seitenkante s ist die Hypotenuse.
◦ Die Hälfte der Bodendiagonalen b ist eine Kathete.
◦ Die gesuchte Höhe ist die andere Kathete.
◦ Es gilt: h² + (0,5b)² = s²
◦ Nach h auflösen gibt:
◦ h = Wurzel aus [s² - 0,25b²]
◦ Einsetzen, fertig.
II Halbe Grundkantenlänge & Seitenflächenhöhe hs
◦ Man hat ein rechtwinkliges Dreieck.
◦ Die Seitenflächenhöhe hs ist die Hypotenuse.
◦ Die Hälfte der Grundkantenlänge a ist eine Kathete.
◦ Die gesuchte Höhe ist die andere Kathete.
◦ Es gilt: h² + (0,5a)² = (hs)²
◦ Nach h auflösen gibt:
◦ h = Wurzel aus [s² - 0,25a²]
◦ Einsetzen, fertig.
Tipps
◦ hs meint nicht h mal s.
◦ hs ist eine einzige Variable.
◦ (0,5a)² gibt aufgelöst 0,25a².
◦ (0,5b)² gibt aufgelöst 0,25b².
◦ Die Bodendiagonale kann man über die Pyramidengrundkanten berechnen.
