Proportionalität erkennen
Anleitung
Basiswissen
Hier werden verschiedene Methoden vorgestellt, wie man überprüfen kann, ob zwei Größen zueinander proportional sind. Was eine Größe in der Mathematik ist und wie proportional definiert ist steht auf der Seite proportional ↗
Beispiel
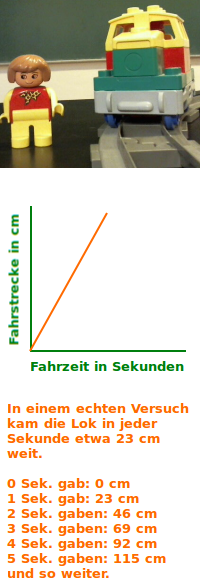
- Eine Spielzeuglok fährt in jeder Sekunde 23 Zentimeter weit.
- Zur Fahrzeit 0 Sekunden gehört die gefahrene Strecke: 0 cm
- Zur Fahrzeit 1 Sekunde gehört die gefahrene Strecke: 23 cm
- Zur Fahrzeit 2 Sekunden gehört die gefahrene Strecke: 46 cm
- Zur Fahrzeit 3 Sekunden gehört die gefahrene Strecke: 69 cm
- Zur Fahrzeit 4 Sekunden gehört die gefahrene Strecke: 92 cm
- Die Fahrzeit und die Strecke sind proportional zueinander.
- Es gibt verschiedene Methoden das zu erkennen.
Konstanter Quotient
- Man nimmt irgendeine Grammzahl, die wirklich vorkommt.
- Man dividiert diese durch die dazugehörige Anzahl.
- Ergibt das immer dieselbe Zahl, dann sind ...
- Grammzahl und Anzahl zueinander proportional:
- 23 durch 1 gibt 23 ⭢ passt
- 46 durch 2 gibt 23 ⭢ passt
- 69 durch 3 gibt 23 ⭢ passt
- 92 durch 4 gibt 23 ⭢ passt
Konstanter Faktor
- Man nimmt irgendeine Anzahl, die wirklich vorkommt.
- Man sucht eine Zahl, mit der man eine Anzahl malrechnen kann, ...
- sodass dann die dazugehörige Grammzahl herauskommt.
- Wenn diese Zahl für alle Werte dieselbe ist, dann ...
- heißt diese Zahl Proportionalitätskonstante.
- Dann ist die Zuordnung sicher proportional.
- 1 mal 23 gibt 23 ⭢ passt
- 2 mal 23 gibt 46 ⭢ passt
- 3 mal 23 gibt 69 ⭢ passt
- 4 mal 23 gibt 92 ⭢ passt
Aus Tabellen
- In Tabellen sind die Anzahlen und Grammzahlen übersichtlich aufgeschrieben.
- Man kann sich aussuchen, ob man den konstanten Quotienten oder Faktor sucht.
- Beide Methoden werden immer zum selben Ergebnis führen.
Aus Graphen
- Eine proportionale Zuordnung ist als Graph leicht zu erkennen.
- Der Graph in einem xy-Diagramm ist immer eine Ursprungsgerade.
- Das heißt: der Graph ist eine Gerade und geht durch (0|0).
- Wenn das so ist, gehört er zu einer proportionalen Zuordnung.
- Siehe auch proportionale Funktion ↗
Verdopplungsprobe
- Wenn man das eine verdoppelt, wird auch das andere doppelt so groß:
- Beispiel: wenn man die Fahrzeit verdoppelt, verdoppelt man auch die Strecke.
- Wenn das mit allen Zahlenpaaren (außer 0|0), dann ist Zuordnung proportional.