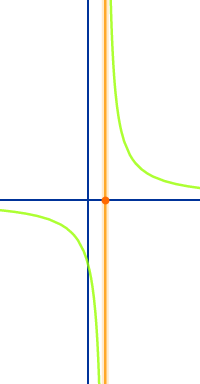
Polstellen bestimmen
Verfahren, wie man Polstellen bestimmt
Basiswissen
Polstellen treten normalerweise bei Funktionen auf, bei denen das x im Nenner steht. Um Polstellen zu finden, setzt man den (oder die) Nenner einer Funktionsgleichung gleich Null. Alle x-Werte, die den Nenner zu Null machen, können Polstellen sein. Wenn die Beträge der Funktionswerte in der Nähe dieser Werte dann in Richtung unendlich wachsen, dann liegt dort wirklich eine Polstelle vor.
Beispiel
- f(x) = x:(x+2)
- Nenner Null setzen: x+2 = 0
- Auflösen: x = -2
- Mögliche Polstelle bei x = -2
- Von links annhähern: f(-2,000001) = 2000001 (über zwei Millionen)
- Von rechts annähern: f(-1,999999) = -1999999 (fast minus zwei Millionen)
- Beobachtung: Nahe bei -2 werden die Beträge der Funktionswerte sehr groß.
- Schluss: Wahrscheinlich ist x = -2 tatsächlich eine Polstelle.