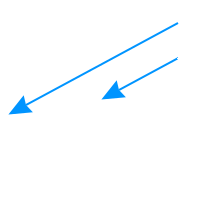
Parallele Vektoren
Ein Vektor ist das (skalare) positive Vielfache des anderen
Was meint skalar hier?
◦ Skalar meint hier: nur mit einer Zahl multiplziert.
◦ Bei Vektoren meint das: Jeder der Komponenten wird mit ein und derselben Zahl malgenommen.
◦ (Nicht skalar wäre die Multiplikation eines Vektors mit einem anderen Vektor.)
◦ Siehe auch => Zahl mal Vektor
Wie sind parallele Vektoren definiert?
◦ Kann man einen Vektor skalar mit einer positiven Zahl malnehmen, sodass als Ergebnis der andere Vektor herauskommt, ...
◦ dann nennt man die beiden Vektoren parallel. Beispiel das Dreifacheinhalbfache des einen Vektors gibt den anderen Vektor.
Welche geometrischen Eigenschaften haben sie?
◦ Sie zeigen in genau dieselbe Richtung.
◦ Sie unterscheiden sich nur in ihrer Länge.
◦ Sie dürfen auch gleich lang sein:
◦ ⮄ ⮅ ⮆ ⮇
Was meint antiparallel?
◦ Antiparallele Vektoren zeigen in entgegengesetzte Richtungen.
◦ Ansonsten unterscheiden sie sich auch nur in ihrer Länge.
◦ Sie dürfen aber auch gleich lang sein:
◦ ⮂ ⮃
Was meint kollinear?
◦ Sowohl parallele als auch antiparallele Vektoren sind immer kollinear zueinander.
◦ Kollineare Vektoren haben entweder genau diesselbe oder genau entgegengesetzte Richtungen:
◦ ⮄ ⮅ ⮆ ⮇ ⮂ ⮃
Siehe auch
=> Antiparallele Vektoren
=> Vektorrechnung [Hauptseite]
=> Vektorrichtung
