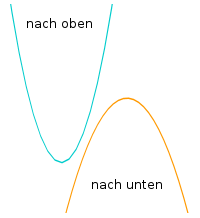
Parabelöffnung erkennen
Für f(x)
Basiswissen
Parabeln als Graph einer quadratischen Funktion können nach oben oder nach unten geöffnet sein. Hier wird erklärt, wie man die Öffnung an der Funktionsgleichung erkennt.
Was meint das am Graph?
- Parabel meint hier den Graph einer quadratischen Funktion.
- Jede Parabel hat eine Mitte: sie ist entweder der tiefste oder der höchste Punkt der Parabel.
- Gehen die Äste von der Mitte weg nach oben, ist die Parabel nach oben geöffnet, ...
- gehen sie nach unten weg, ist die Parabel nach unten geöffnet.
- Siehe auch Parabel ↗
Was meint das für die Gleichung?
- Zu jeder quadratischen Funktion kann man eine Funktionsgleichung angeben.
- An der Gleichung kann man auch ohne Graph die Öffnung erkennen.
- Dazu formt man die Gleichung erst in eine Standard-Form um.
- Welche dieser Standardformen man nimmt, das ist egal.
- Dann kann man die Öffnung an der Gleichung ablesen:
Allgemeine Form
- y = ax² + bx + c
- ax² meint dasselbe wie a·x².
- Das a ist die Zahl vor dem x².
- Ist a positiv, ist die Parabel nach oben geöffnet.
- Ist a negativ, ist die Parabel nach unten geöffnet.
- Ein x² ohne a meint: a=1
- -x² meint: a=-1
Scheitelpunktform
- y = a(x-d)² + e
- a(x-d)² meint dasselbe wie a·(x-d)²
- Das a ist die Zahl vor der Klammer.
- Ist a positiv, ist die Parabel nach oben geöffnet.
- Ist a negativ, ist die Parabel nach unten geöffnet.
- Ein x² ohne a meint: a=1
- -x² meint: a=-1
Normalform
- y = x² + px + q
- Wichtig: vor dem x² ist kein Faktor.
- Die Parabel ist immer nach oben geöffnet
Beispiele
- y = 4x² + 18x - 24 - 3(2x²+4)
- Rechte Seite erst vereinfachen ...
- y = 4x² + 18x - 24 - 6x² - 12 ...
- Und Teilglieder zusammenfassen:
- y = -2x² + 18 x - 36
- Das ist die allgemeine Form.
- a ablesen: -2
- Also: nach unten geöffnet
Tipps
- Klammern immer auflösen: 2[x²+4] ⭢ 2x²+8
- Minus mal minus beachten: -3(-x²+4) ⭢ 3x²+12
- Zusammenfassen: -3x² + 16 + 5x² ⭢ 2x² + 16
- Binomische Formel nutzen: (a+b)² = a² + 2ab + b²