Nullstellen von quadratischen Funktionen
Begriffsklärungen
Basiswissen
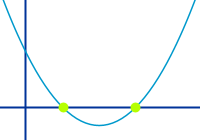
Nullstellen sind immer x-Werte auf der x-Achse. Es sind die x-Werte, bei denen ein Funktionsgraph die x-Achse schneidet oder berührt. Das wird hier näher für Parabeln erklärt.
Was ist ein quadratische Funktion?
- Eine quadratische Funktion heißt manchmal auch Parabelgleichung.
- Quadratische Funktionen gehören zu den ganzrationalen Funktionen.
- Jede Funktion, die man zu f(x) = Ax² + Bx + C umformen kann heißt quadratisch.
- A, B und C sind dabei irgendwelche Zahlen, egal ob dezimal oder negativ.
- Beispiel in faktorisierter Form: f(x) = 0,5(x-1)(x-3)
- Beispiel in allgemeiner Form: f(x) = 0,5x²-2x+1,5
Was sind Nullstellen?
- Im Graph sind das die x-Werte, bei denen der Graph durch die x-Achse geht.
- Nullstellen sind auch die x-Werte, bei denen der Funktionswert 0 wird.
- Der Funktionswert wird oft mit f(x) oder auch y abgekürzt.
- Beispiel: wenn man in f(x) = 0,5x²-2x+1,5 für x die 3 einsetzt ...
- dann kommt für den Funktionswert 0 heraus. Also ist bei x=3 eine NS.
Wie erkennt man Nullstellen graphisch?
- Das sind die Stellen, wo der Graph die x-Achse berührt oder schneidet.
- Die Nullstelle ist immer nur der x-Wert, davon.
- Nullstellen heißen auch x-Achsenabschnitte.
Was meint "Nullstellen von Parabeln"?
- Der Graph einer quadratischen Funktion heißt Parabel.
- Nullstellen von quadratischen Funktionen und Parabeln meint dasselbe.
- Wenn man von Parabeln spricht, betont man eher den graphischen Ansatz.
- Wenn man von Funktionen redet, dann geht es mehr um die reinen Zahlen.
- Aber die beiden Worte werden oft im gleichen Sinn verwendet.
Wie viele NS haben quadratische Funktionen?
- Es gibt drei Möglichkeiten: keine, eine und zwei.
- Oft sieht man das gut an der Funktionsgleichung.
Wie kann man die Nullstellen bestimmen?
- Es gibt viele verschiedene Verfahren.
- Diese sind auf einer eigenen Seite erklärt.
- Das bekannteste Verfahren ist die pq-Formel ↗
- Mehr dazu unter Nullstellen von quadratischen Funktionen bestimmen ↗
Beispiele
- f(x) = 0,5x²-2x+1,5; NS bei x=1 und bei x=3.
- f(x) = x²-4; NS bei x=-2 und eine bei x=2.
- f(x) = x²; NS bei x=0.
- f(x) = x²+4; Keine NS