Nullstellen von Geraden bestimmen
Methoden
Basiswissen
Graphisch durch ablesen, über Umformen berechnen oder auch probieren: es gibt verschiedene Methoden, die hier kurz vorgestellt sind.
Was heißt Nullstelle?
- Wo eine Gerade die x-Achse schneidet hat sie eine Nullstelle.
- An der Nullstelle ist der y-Wert (auch f(x) genannt) immer 0.
- Daher der Name. (Der x-Wert muss nicht Null sein).
- Es gibt verschiedene Möglichkeiten, Nullstellen zu finden:
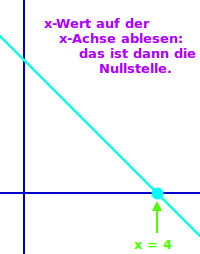
Graphisch (ablesen)
- Wenn man den Graphen hat, kann man die Nullstellen ablesen.
- Finde den Punkt, an dem die Gerade die x-Achse schneidet.
- (Die x-Achse geht von links nach rechts.)
- Der x-Wert dort ist die Nullstelle.
Probieren
- Nimm die Funktionsgleichung, z. B. y=4x-20
- Wenn dann bei einer dieser x-Zahlen für y Null rauskommt, ...
- dann ist x-Zahl die gesuchte Nullstelle.
- Bei x=8 hätte man im Beispiel oben keine NS.
- Bei x=5 aber wird y zu 0.
- x=5 ist die Nullstelle.
Berechnen
- Man hat die Gleichung in der Form y=mx+b.
- Das y meint dasselbe wie f(x).
- Man setzt für y die Zahl 0 ein.
- Dann hat man eine Gleichung mit x als einziger Unbekannten.
- Dann stellt man die Gleichung nach x um.
- Der gefundene x-Wert ist die Nullstelle.
- Ausführlicher unter Nullstellen von Geraden berechnen ↗
Keine Nullstelle
- Es gibt auch Geraden, die keine Nullstelle haben.
- Solche Geraden sind immer parallel zur x-Achse.
- Sie laufen also von links nach rechts.
- Und: sie gehen nicht durch den Punkt (0|0).