Lineare Abbildung
Graphisch
Basiswissen
Eine lineare Abbildung oder lineare Transformation wird oft in Verbindung mit Veränderungen von 2D- oder 3D-Figuren über Matrizen behandelt. Diese Anwendung wird hier kurz vorgestellt.
Einführung
Bei einer linearen Abbildung werden Vektoren von einer gegebenen Figur nach festen Regeln zu neuen Vektoren eines Bildes umgeformt. Diese Regel wird oft in Form einer Matrix geschrieben. Möchte man Punke in einem Koordinatensystem transformieren, schreibt man sie in Form ihrer Ortsvektoren.
Beispiel
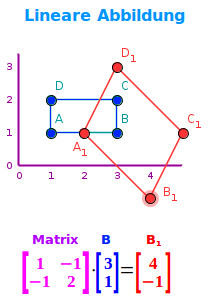
Man stelle sich ein xy-Koordinatensystem vor. In ihm werden vier Punkte definiert: A(1|1), B(3|1), C(3|2) sowie D(1|2). Diese vier Punkte bilden die Ecken eines Rechtecks. Jeder der Punkte kann auch als Ortsvektor gedacht werden. Nun sei eine quadratische Matrix gegeben: (1,1|-1,2). Die ersten zwei Zahlen entsprechen der ersten Zeile, die letzten zwei Zahlen der zweiten Zeile. Nun kann man diese Matrix mit jedem einzelnen der Eckpunkt-Vektoren multiplizieren. Dabei entstehen vier neue Punkte: A'(2|1), B'(4|-1), C'(5|1) sowie D'(3|3). Diese vier neuen Punkte haben das ursprüngliche Rechteck zum einen gedreht und zum anderen in ein schiefes Parallelogramm verwandelt. Es gibt nun bestimmte Matrizentypen, die immer zu bestimmten Typen einer Abbildung oder Transformation gehören.
Matrizentypen 2D
- 90°-Drehung gegen den Uhrzeigersinn: (0;-1|1;0)
- Drehung um den Winkel θ gegen die Uhr: (cosθ;-sinθ|sinθ;cosθ) Drehmatrix ↗
- Spiegelung an der x-Achse: (1;0|0;-1)
- Spiegelung an der y-Achse: (-1;0|0;1)
- Spiegelung an Gerade mit Winkel θ: (cos2θ;-sin2θ|sin2θ;cos2θ)
- Vergrößerung um Faktor 2: (2;0|0;2)
- Horizontale Scherung: (1;m|0;1)
- Horizontale Stauchung: (k;0|0;1/k)
- Projektion auf y-Achse: (0;0|0;1)