Keine Funktionen
Beispiele für Zuordnungen, die aber keine Funktionen sind
Basiswissen
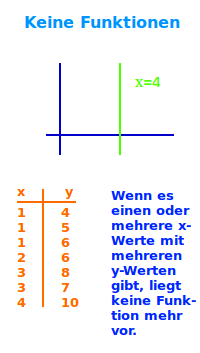
Wenn zu einem x-Wert mehrere y-Werte gehören, dann liegt keine Funktion sondern nur noch eine Relation (Zuordnung) vor. Hier einige Beispiele dazu.
y²=x
- Es gibt x-Werte, zu denen zwei y-Werte passen.
- Beispiel: zu x=9 würden y=-3 und y=3 passen.
- Also: keine Funktion
Telefonnummern
- Man hat eine Telefonbuch.
- Links steht jeweils ein Name.
- Rechts stehen alle Telefonnummern zu diesem Namen.
- Zu einem Namen können also mehrere Telefonnummern passen.
- Man sagt: die Telefonnummern sind keine Funktion des Namens.
- Das meint: Zu einem Namen gehört nicht eindeutig nur eine Nummer.
- Also: keine Funktion
Weidefläche
- Grundlage des Gedanken ist die Idee der Weideflächenmaximierung ↗
- An einem geraden Fluss soll eine rechteckige Weidefläche abgegrenzt werden.
- Dazu steht ein Zaun einer festen Gesamtlänge l zur Verfügung.
- Am Fluss entlang ist kein Zaun nötig, man muss nur drei Seiten einzäunen.
- Die Fläche hat dann eine Breite b senkrecht zum Fluss und ...
- eine Länge l parallel zum Fluss. Man kann eine Formel finden ...
- mit der man für jede mögliche Breite b den Flächeninhalt A berechnen kann.
- Die Umkehrung gilt aber nicht: zu jedem möglichen Flächeninhalt A ...
- gibt es immer zwei unterschiedliche Breiten b die passen.
Kistenvolumen
- Grundlage des Gedanken ist die Idee der Pappkistenvolumenmaximierung ↗
- Aus einem quadratischen Stück Pappe soll durch Schneiden und Falten ...
- eine deckellose quaderförmige Pappkiste entstehen.
- Für jeden bestimmten Zuschnitt kann man eindeutig das Volumen berechnen.
- Die Umkehrung gilt aber nicht: zu jedem Volumen gibt es mehrere Zuschnitte.
Senkrechter Wurf
- Man wirft einen Ball senkrecht nach oben.
- Man kann für jeden Zeitpunkt eine Höhe des Balles angeben.
- Die Höhe wäre also eine eindeutige Funktion der Flugzeit.
- Die Umkehrung des Gedankens gibt aber keine Funktion:
- Für (fast) alle Höhen kann man immer genau zwei Zeiten angeben:
- Einmal beim Hochfliegen und einmal beim Herunterkommen.
- Die Flugzeug ist also keine eindeutige Funktion der Höhe.
- Wenn man nur die Höhe kennt, dann kann man nicht sicher sagen ...
- zu welcher Zeit nach dem Abwurf sich der Ball gerade befindet.
- Also: keine Funktion