Integrationsgrenzen
Definition
Basiswissen
Die Integrationsgrenzen, auch Integrationsränder genannt, sind immer zwei x-Werte. Der linke Rand wird oft a genannt, der rechte oft b. Hier wird die anschauliche Bedeutung davon erklärt.
Anschaulich
- Die Flächenbilanz zwischen linkem und rechtem Rand:
- Man hat eine Funktion f(x) mit ihrem Graphen in einem Koordinatensystem.
- Man denkt sich zwei unterschiedliche Stellen auf der x-Achse aus:
- Die linke Stelle, z. B. bei x=4 ist der linke Integrationsrand.
- Die rechte Stelle, z. B. bei x=8 ist der rechte Integrationsrand.
- Die Reihenfolge ist wichtig, sie darf nicht vertauscht werden.
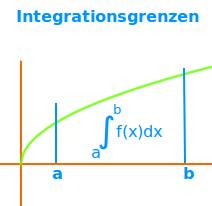
- Man zieht dann je einen senkrechten Strich durch a und b.
- Dadurch ist eine an vier Seiten umgrenzte Fläche entstanden:
- Oben und unten sind die Flächengrenzen die x-Achse und der Graph.
- Rechts und links sind die Grenzen die senkrechten Striche durch a und b.
- Die genaue Bedeutung dieser Fläche wird behandelt unter Flächenbilanz ↗
- Der Inhalt dieser Fläche wird berechnet über ein bestimmtes Integral ↗
Rechnerisch
- Man berechnet das bestimmte Integral von f(x) in den Grenzen von a und b.
- Geschrieben wird das mit Hilfe des Integralzeichen mit f(x) und dx dahinter.
- An das untere Ende des Integralzeichens schreibt man die linke Grenze a.
- An das obere Ende des Integralzeichens schreibt man die recht Grenze b.
- Wie man das berechnet steht unter Bestimmtes Integral berechnen ↗
Uneigentlich
- Es gibt auch den Fall, dass eine Integrationsgrenze "unendlich" ist.
- Mehr dazu unter uneigentliches Integral erster Art ↗