Grenzwert
Analysis
Basiswissen
Von einem Grenzwert[1] oder Limes[7] spricht man bei Folgen, Reihen und Funktionen. Hier wird erklärt, wie der Grenzwert im Sinne der Mathematik exakt definiert ist.
Definition von Grenzwert über die Epsilon-Umgebung
Der Grenzwert einer Funktion f(x) ist diejenige Zahl z an die sich bei größer werdendem x-Werten die Funktionswerte f(x) oder y immer weiter annähern, und zwar so, dass man immer einen x-Wert angeben kann, ab dem bei weiter wachsendem x-Wert die Funktionswerte f(x) immer kleiner sind als z+ε und immer größer als z-ε. Das muss für jeden noch so beliebig klein gedachten Wert von ε gelten, wobei aber ε immer positiv bleiben muss, also niemals genau 0 oder kleiner als 0 sein darf[8][9].
Falsche Vorstellungen im Zusammenhang mit einem Grenzwert
Man trifft im Umfeld der Schulmathematik verschiedene Definitionen des Grenzwertes an, die historisch gewachsenen, intuitiven Vorstellungen entsprechen, aber nicht mit der exakten Definition übereinstimmen. Dazu stehen hier einige Beispiele.
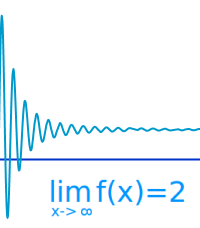
- Der Unterschied zwischen dem Grenzwert und dem Funktionswert wird für wachsende x immer kleiner und ist irgendwann unendlich klein[1]: Richtig ist, dass der Funktionswert auch für wachsende x lokal immer mal wieder größer werden darf, etwa bei oszillierenden Funktionen. Es macht keinen Sinn davon zu sprechen, dass "irgendwann" der Unterschied unendlich klein ist, da sich kein eindeutiges Kriterium angeben lässt, ab wann genau man von unendlich klein sprechen soll. Ist ein Milliardstel unendlich klein? Oder erst ein Trillionstel? Die hier vorliegende Intuition wird richtig gefasst über die sogenannte Epsilon-Umgebung ↗
- Der Funktionswert und der Grenzwert fallen für ausreichend große Werte von x irgendwann einmal zusammen[3]: Richtig ist, dass der Funktionswert und der Grenzwert zusammen fallen dürfen, also derselbe Wert sein dürfen, aber nicht müssen. So wird der Funktionswert von f(x)=1/x bei gegen unendlich wachsenden x-Werten niemals exakt 0 sein, dennoch ist die Zahl 0 der Grenzwert für x gegen unendlich. Siehe dazu auch den Graphen der dazugehörigen Normalhyperbel ↗
- Die Funktion nähert sich dem Grenzwert immer weiter an, wird ihn aber nie erreichen[10]. Richtig ist, dass der Grenzwert durchaus angenommen werden darf, etwa bei oszillierenden Funktionen. Auch gilt zum Beispiel für die konstante Funktion f(x)=2 dass ihr Grenzwert überall die Zahl 2 selbst ist.
Die Funktion als Beispiel
- Man hat eine Funktion f(x) gegeben.
- Die zentrale Frage ist dann: was passiert mit dem y-Wert, …
- wenn man mit dem x-Wert immer weiter in eine bestimmte Richtung geht?
- Zum Beispiel: was passiert mit den y-Werten wenn bei der Funktion f(x)=2+1/x …
- die x-Werte immer größer werden, also gegen unendlich gehen?
- Formal schreibt man etwas wie: x ⭢ 0 oder x ⭢ unendlich
Eine pragmatische Beschreibung
Der Grenzwert wird sinngemäß oft als eine Zahl beschrieben, der man sich immer mehr annähert, die man aber nie erreicht. Richtig ist, dass man einem Grenzwert immer näher kommt, wenn man zwei Dinge mit berücksichtigt. a) Man kann sich bei der Annäherung auch wieder ein Stück vom Grenzwert entfernen. Man kann sich ihm sozusagen auch in Schlängenkurven annähern. Und b) der Grenzwert selbst darf auch kurzfristig oder sogar dauerhaft erreicht werden. So ist der korrekte Grnenzwert der Funktion f(x)=4 für x gegen unendlich einfach nur die Zahl 4. Mathematisch exakt fassen lässt sich die Idee eines Grenzwertes mit der Idee einer Umgebung.
Die exakte Definition
- Man hat eine Funktion f(x) gegeben. Der Funktionswert sei das y.
- Man denkt sich dann eine beliebige positive Zahl aus und nennt sie Epsilon.
- Man wählt Epsilon dabei in der Regel sehr klein, zum Beispiel: Epsilon = 0,0002
- Geht man auf der x-Achse in Richtung größerer x-Werte, dann muss es einen ...
- x-Wert geben, ab dem der Abstand von y zum vermuteten Grenzwert …
- niemals mehr größer sein wird als das angenommene Epsilon.
- Man kann also weiter in Richtung unendlich gehen, aber …
- die y-Werte sind nie weiter weg vom Grenzwert als die Zahl Epsilon.
- Wenn diese Bedingung für beliebig kleine Werte von Epsilon gilt, …
- dann war der angenommene Grenzwert auch der tatsächliche Grenzwert.
- Siehe auch Epsilon-Umgebung ↗
Beispiel f(x) = 1/x
- Man betrachte die Funktion: f(x) = 1/x
- f(1) ist 1; f(2) gibt 0,5; f(10) gibt 0,1 und so weiter.
- Der dazugehörige Graph ist die sogenannte Normalhyperbel ↗
- Der Graph fängt bei kleinen x-Werten mit sehr hohen y-Werten an.
- Geht man auf der x-Achse weiter nach rechts, werden die y-Werte immer kleiner.
- Der Graph nähert sich von oben der x-Achse an, erreicht diese aber nie.
- An diese Beispiel kann man die folgende exakte Grenzwertdefinition betrachten.
- Man wählt eine Zahl, von der man vermutet oder weiß dass sie der Grenzwert ist.
- Bei der Funktion f(x)=1/x ist der vermutete Grenzwert die Zahl 0.
- Man wählt einen kleinen Wert für Epsilon, z. B.: 0,5
- Man sucht einen x-Wert, ab dem die y-Werte immer näher als 0,5 am Grenzwert liegen.
- Das ist die Zahl x=2. Ab x=2 liegen alle y-Werte näher als 0,5 am Grenzwert.
- Diese Regel soll nun für beliebig kleine Epsilon-Werte funktionieren.
- Ab welchem x-Wert liegt y zum Beispiel nie weiter als 0,00001 vom Grenzwert entfernt?
- Wieder kann man dafür einen bestimmten x-Wert angeben, hier: eine Million
- Egal wie klein man Epsilon wählt, man wird immer einen passenden x-Wert finden.
- Wenn das für einen angenommenen Grenzwert machbar ist, dann …
- ist der angenommene auch der tatsächliche Grenzwert.
- Für f(x) = 1/x ist der Grenzwert tatsächlich: 0
Synonyme
===== Fußnoten
- [1] In einem Lexikon, 1906: "Grenzwerte. Unter Grenze versteht man den Abschluß einer ins Unendliche fortschreitenden Vorstellungsreihe durch eine neu hinzugedachte Vorstellung. In diesem Sinne ist 1/3 der Grenzwert, welchem die Reihe der Brüche 0,3, 0,33, 0,333, 0,3333 ... sich immer mehr annähert. Man schreibt daher geradezu lim 0,3333 ... = 1/3. Dabei wird die Differenz zwischen dem n ten Wert der Reihe und dem Grenzwert mit zunehmendem n immer kleiner, zuletzt unendlich klein; sie kann ferner immer positiv oder immer negativ oder endlich bald positiv, bald negativ sein." In dem Artikel folgen dann noch weitere mathematische Beispiel. In: Lueger, Otto: Lexikon der gesamten Technik und ihrer Hilfswissenschaften, Bd. 4 Stuttgart, Leipzig 1906., S. 626. Online: http://www.zeno.org/nid/20006036031
- [2] Ein anderes Lexikon (1907) betrachtet den mathematischen Grenzwert unter Grenze, heute spräche man von einer Schranke: "Grenzwert (Limes), in der Mathematik, s. Grenze. – In der Nationalökonomie bezeichnet man mit G. (Grenznutzen, engl. Final degree of utility) den Wert, den von einer Menge von Gütern gleicher Art die letzte Einheit für einen Menschen hat." In: Meyers Großes Konversations-Lexikon, Band 8. Leipzig 1907, S. 281. Online: http://www.zeno.org/nid/20006709958
- [3] "Grenzwert ist eine unveränderliche Größe, der sich eine veränderliche so weit nähern kann, daß sie zuletzt mit derselben zusammenfällt. (Bonnel, les limites et l'atome.)" In: Kirchner, Friedrich / Michaëlis, Carl: Wörterbuch der Philosophischen Grundbegriffe. Leipzig 1907, S. 249. Online: http://www.zeno.org/nid/20003583163
- [4] Vogt, Der Grenzbegriff in der Elementarmathematik, Breslau 1885.
- [5] Kerry, System einer Theorie der Grenzbegriffe, Bd. 1, Wien 1890.
- [6] Dubois-Reymond, P., Die allgemeine Funktionentheorie, Bd. 1, Tübingen 1882.
- [7] Limes als Grenzwert im Sinn der Mathematik ist seit spätestens dem Jahr 1905 in Gebrauch: "Limes (lat., »Grenze«), in der Mathematik soviel wie Grenzwert." In: Meyers Großes Konversations-Lexikon, Band 12. Leipzig 1908, S. 557. Siehe auch Limes ↗
- [8] Der Bronstein definiert in Anlehnung an Augustin-Louis Cauchy (1789 bis 1857): "Damit eine Funktion f(x) an der Stelle x=a einen Grenzwert besitzt, ist es notwendig und hinreichend, dass sich die Funktionswerte f(x₁) und f(x₂) für zwei beliebige Werte x₁ und x₂ der unabhängigen Variablen, die zum Definitionsbereich gehören und in hinreichender Nähe von a liegen, beliebig wenig voneinander unterscheiden." In: Bronstein, Semendjajew, Musiol, Mühlig: Taschenbuch der Mathematik. 10. Auflage, 2016. ISBN: 978-3-8085-5789-1. Verlag Harri Deutsch. Dort die Seiten 54 und 55. Siehe auch Der Bronstein ↗
- [9] Als exakt für den Grenzwert einer Funktion an einer Stelle bezeichnet der Bronstein die folgende Definition: "Damit eine Funktion f(x) an der Stelle x=a einen Grenzwert besitzt, ist es notwendig und hinreichend, dass sich nach Vorgabe einer beliebig kleinen positiven Zahl ε eine zweite positive Zahl η [kleines Eta] angeben lässt, sodass für zwei beliebige Werte x₁ und x₂ aus dem Definitionsbereich, die den Bedingungen |x₁ - a| < η und |x₂ - a < η genügen, die folgende Bedingung erfüllt ist: |f(x₁) - f(x₂) | < ε." In: Bronstein, Semendjajew, Musiol, Mühlig: Taschenbuch der Mathematik. 10. Auflage, 2016. ISBN: 978-3-8085-5789-1. Verlag Harri Deutsch. Dort die Seite 55. Der Bronstein behandelt daneben noch Grenzwerte von bestimmten Integralen, Folgen in einem metrischen Raum, von Funktion mit komplexen Veränderlichen, mehreren Veränderlicher und auch von Reihen. Siehe auch Der Bronstein ↗
- [10] Für falsch halten wir zum Beispiel die Definition: "Der Grenzwert ist ein Zahlenwert, welchem eine Funktion, Reihe oder Folge entgegenstrebt, ihn jedoch nie erreicht." Wäre die Definition richtig, hätte f(x)=2 für x gegen unendlich nicht die Zahl 2 als Grenzwert. In: StudySmarter. Dort der Artikel "Grenzwerte". Abgerufen am 14. Dezember 2023. Online: https://www.studysmarter.de/schule/mathe/analysis/grenzwerte/